Twist and Shout

Orbital dynamics, that is, the motion of planets and stars about each other, is deeply dependent on computational modelling. The basic motion of one planet or star about another (the so-called two body problem) is fairly simple, and can be summarized by Kepler’s laws of planetary motion, the motion of multiple planets and stars is extraordinarily complex. In fact while the two-body problem is almost trivial to solve, the three-body problem has no exact general solution. As soon as you have three or more masses in your system, the motion can be highly chaotic.

There are, however, some broad patterns we see in many-body systems, such as resonances and the formation of gaps in the asteroid belt. There are also interesting effects that have some surprising consequences. One of these effects is known as the Kozai mechanism.

Within orbital dynamics there are certain properties such as energy and angular momentum that are conserved (or approximately conserved). This means mathematically that certain properties of a system are constants. The Kozai mechanism deals with a quantity related to angular momentum known as Lz. This quantity is a constant, and it relates how elliptical an object’s orbit is (its eccentricity) to the orientation or tilt of its orbit (its inclination).

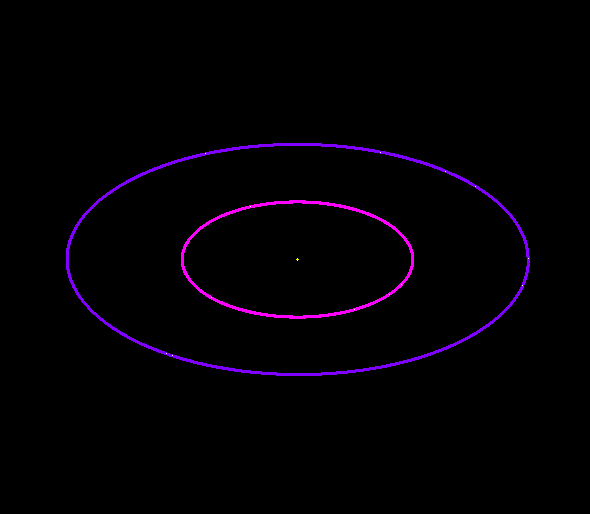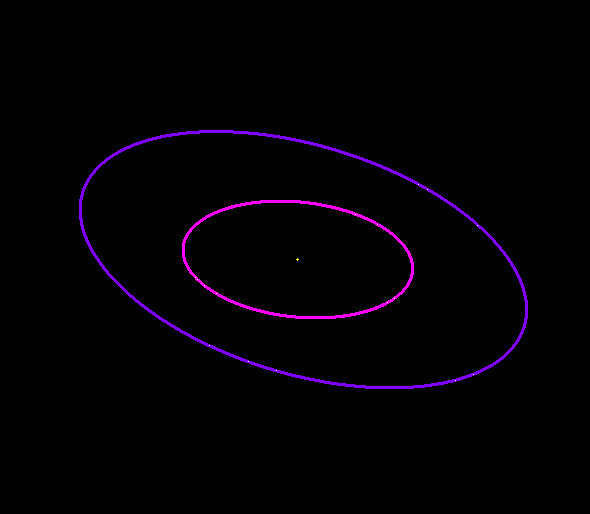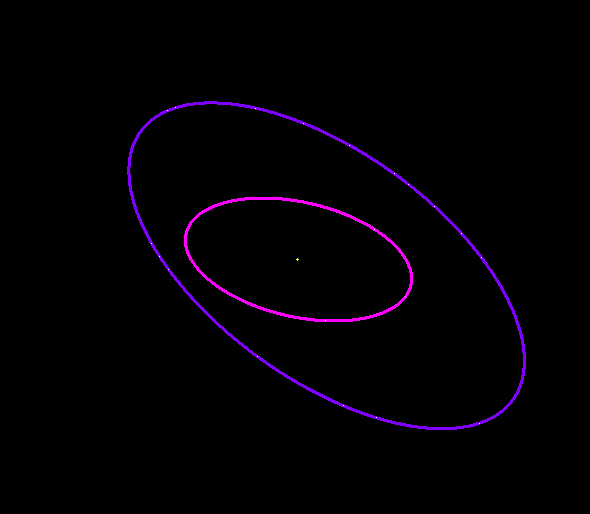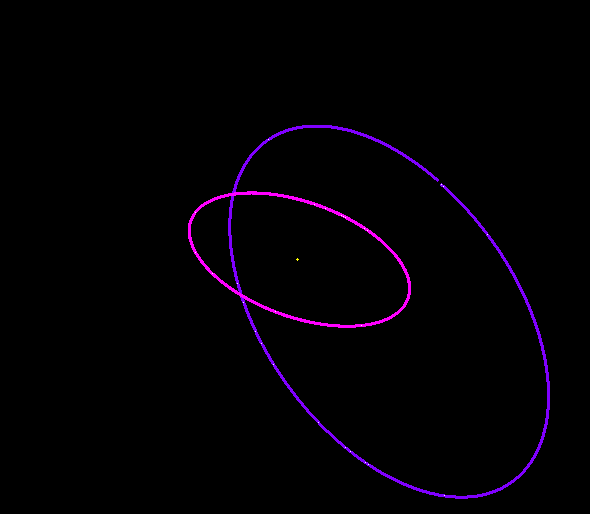Gravity Simulator

You can get an idea of how these are related by imagining a flexible hula hoop. If you hold the hoop in front of you, aligned vertical to the ground, then the hoop will look like a circle to you. If you tilt the hoop at an angle to the ground, then it will look like a squashed oval to you. Now, if you wanted to move the hula hoop vertical again, but keep it looking like an oval, then as you tilt it vertical you have to squash the hoop itself. To keep the apparent shape constant, if you change the angle, you also have to change how much the hoop is squashed. The Lz property is similar, in that the eccentricity and inclination can change in relation to each other, but the “apparent shape” (Lz) stays constant.

The Kozai mechanism does just that. Basically it is a resonance between a smaller object and a larger object that causes the smaller object’s orbit to change its inclination to become more aligned with the larger object, and doing so at the cost if increasing the eccentricity of its orbit. The effect is a little hard to visualize, but you can see an example in the image above. The central dot is a star, and the orbits of two planets are shown. Outside of view is a second star orbiting at a different angle from the planets. You can see how the orbit of the outer planet is gradually shifted due to the second star.

One of the ways the Kozai mechanism comes into play is between the orbits of Neptune and Pluto. Gradually Pluto’s orbit is being tilted toward the orbital plane of Neptune. As a result, the eccentricity of Pluto’s orbit increases. This can explain why Pluto’s orbit is so elliptical, while most of the other planets are not. Another consequence of this mechanism is that the point of Pluto’s closest approach to the sun (its periapsis) is shifted relative to Neptune’s, which is part of the reason why Pluto will never collide with Neptune even though it crosses Neptune’s orbit.

A similar resonance should occur with other minor planets similar to Pluto (the Plutoids). This means that their orbits should be clustered rather than randomly distributed. We already see that with other minor planets such as Makemake.

All due to an interesting orbital resonance.