Tully-Fisher King

Measuring the distance to galaxies can be tricky. If a galaxy is fairly close, then we can look for a type of variable star known as a Cepheid variable. These stars vary in brightness proportional to its absolute magnitude. Since we can calculate the absolute magnitude of a Cepheid variable, we can observe its apparent brightness and calculate its distance since the further an object is the dimmer it appears. Cepheid measurements let us measure the distance of galaxies in our Local Group and a bit further.

For more distant galaxies we can’t use this method. Instead we have to hope for a supernova to occur in a given galaxy. One kind of supernova (known as type Ia) has a very consistent absolute magnitude. So if such a supernova occurs in a distant galaxy we can observe its apparent brightness and determine the galaxy’s distance.

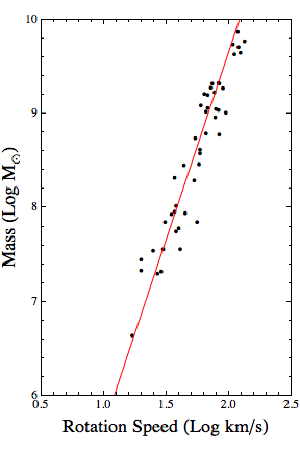
BK

But suppose we have a galaxy that is too far to observe Cepheid variables, and it hasn’t had any type Ia supernova. If the galaxy is a spiral galaxy, then we can make a reasonable estimate of its distance using a pattern known as the Tully-Fisher relation. This was first observed in 1977, and noticed a simple correlation between the brightness of a galaxy and the range of stellar speeds within the galaxy. For spiral galaxies, its brightness is proportional to its total mass, and since spiral galaxies all have basically the same shape the range of fast central stars to slow stars on the galactic rim tends to be proportional to the mass as well. I’ve plotted a set of galaxies in the figure, and you can see there is a good relation between the two.

What this means is that you can measure the distribution of stellar speed in a spiral galaxy, which is fairly easy to do using the Doppler effect. By the Tully-Fisher relation you then have an idea of the absolute magnitude of the galaxy, which you can compare to the apparent brightness of the galaxy to estimate its distance.

As you can see from the graph, the relation isn’t exact. Spiral galaxies aren’t identical, so the Tully-Fisher relation is only approximate. We’d prefer to observe a supernova in the galaxy, but Tully-Fisher can give a reasonable estimate.