Problematic

Newton’s law of gravity takes a bit of calculus to really wrap your head around it, but the basic relation is very simple. Every pair of masses in the universe experiences a mutual gravitational attraction, each feeling the pull of the other’s gravitational field. The force of attraction is mutual, which leads to some interesting consequences. For example, when you step on the scale in the morning, you are weighing yourself in the Earth’s gravitational field. You are also weighing the Earth in your gravitational field. Your weight is also the Earth’s weight in your gravity.

The strength of that attraction depends on the size of the two masses and the distance between them, following a relation known as the inverse square law. Suppose two masses feel a force of 100 Newtons between them. If you double their distance of separation, then they would feel a force of only 25 Newtons, a fourth of their initial force. It’s a remarkably simple relationship.

But there’s a gravitational force between every pair of masses in the universe, which is where things can get complicated. In order to calculate the motion of an object in general, you would need to determine the gravitational attraction from all the other masses in the area, and you need to determine how those masses are gravitationally affected by the object. There are lots of ways to simplify things a bit. After all, the largest and closest masses will have the greatest effect on an object, so usually you can ignore the gravity of distant objects. When calculating the motion of the Moon, for example, you don’t have to worry about the gravity of the Andromeda galaxy.

But even with simplifications there is still a problem. While we have a simple general solution for the motion of two masses acting under their own gravity, we don’t have a general solution for three masses. We just can’t determine the exact motion for three masses moving in general ways. This is known as the 3-body problem, and it is problematic.

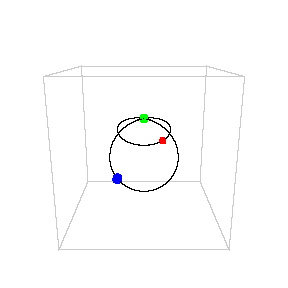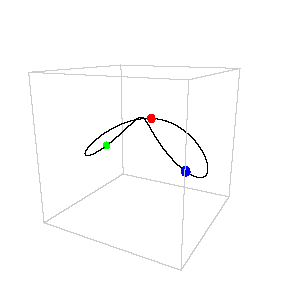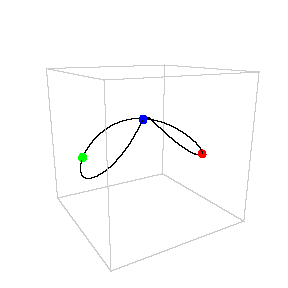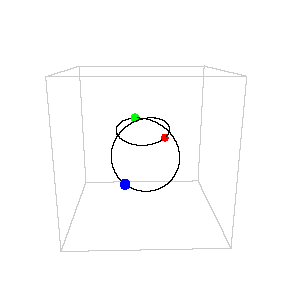Chris Moore

This doesn’t mean we can’t predict the motion of three or more massed acting under gravity. We can actually predict motions quite well, just not exactly. For 3-body systems like the Sun, Earth and Moon we can describe the motion very precisely. We’ve also found some interesting exact solutions to the 3-body problem for specific cases, such as three equal masses moving along a common orbit as seen in the figure here.¹

We can find specific solutions for three or more masses, but we can’t find a complete general solution. Instead we find approximate solutions, or determine solutions computationally. Normally this isn’t too much of a problem, but there are cases where the future motion of an object is extremely sensitive to its current position. This can be particularly true for the case of a small mass in a complex gravitational field.

Of course Newton’s gravity is an approximation of Einstein’s general relativity, but in general relativity it gets worse. We can calculate the motion of an object in the gravitational field of another (such as the motion of Mercury in the Sun’s gravitational field), but the general 2-body solution can’t be done in general. If we want to calculate the motion of two orbiting neutron stars, for example, we must do it computationally. That means there are no general exact solutions in GR.

Sometimes in astrophysics a simple idea can be quite problematic.