The Old Model
Doesn’t Work

Queens University

Astrophysics is mainly about gravity. Yes, it also depends upon chemistry, nuclear physics, optics and the like, but gravity is the overarching force. Gravity drives stars to shine, it drives black holes to form, and it drives the motion of stars and planets. So a good understanding of the universe depends upon a good understanding of gravity.

We have a really good understanding of gravity. Newtonian gravity, which describes the force between masses, allows us to calculate the motion of planets to extraordinary precision. Newton’s gravity is so precise that we can use it to predict the motion of probes that travel to the various planets. We’ve observed the gravitational interaction of masses in the lab, and they agree with Newton as well.

For large masses or high energies, we require Einstein’s approach to gravity. Einstein’s model treats gravity as a curvature of space and time instead of a force, but this strange view has been supported by observation. We have seen the precession of Mercury’s orbit, the bending of light by gravitation, and the twisting of space around rotating masses. Einstein’s general relativity works incredibly well. It has passed the scientific test time and again.

While Einstein’s model is often portrayed as an overthrowing of Newton’s model, this isn’t an entirely accurate view. True, Einstein interprets the mechanism of gravity in a radically different way than Newton, but the resulting motion predicted by each model is quite similar. For large dense masses Einstein is more accurate, but for “everyday” objects such as planets and moons, the models of Newton and Einstein are almost indistinguishable. In many ways, Einstein is a generalization of Newton that improves the accuracy. Our gravitational theory works, and is supported by countless experiments.

One of the well established properties of gravity is that it is stronger when objects are close and weaker when objects are more distant. We see this not only in the lab, but in the motion of the planets. Mercury zips around the Sun at a speed of more than 100,000 miles per hour (45 km/s), while Neptune traverses its orbit at a speed of only 12,000 miles per hour (5 km/s). The reason for this is because Mercury is much closer to the Sun (which contains most of the mass in the solar system) than Neptune, so it must move much faster to overcome the much stronger gravitational attraction.

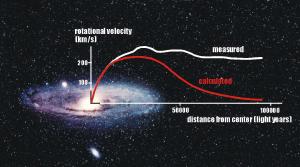
One would expect to see a similar trend in the motion of stars within a galaxy. Most galaxies have a central bulge where most of the stars (and therefore most of the mass) of the galaxy lie. One would therefore expect that stars just outside the central bulge would move much faster than stars on the outer edge of a galaxy. This is not what we observe, as you can see in the image above, which plots the observed speed of stars as a function of their distance from galactic center vs the expected speed calculated by gravitational theory and the observed distribution of mass in a galaxy.

It’s pretty clear that the difference isn’t small, it’s huge. The speed of stars far from the center in this case (the Andromeda galaxy) is just as fast as stars near the center. For some galaxies the distant stars actually move faster than the close stars. The difference between observation and theory isn’t minor. The two are in complete disagreement. We see this not in one galaxy, but in galaxy after galaxy. The theory never matches observation.

What’s important to understand here is that this is not due to poor measurement. We can observe not only the starlight in the visible spectrum (such as in the image below), but also in infrared, ultraviolet, radio and x-rays. Observing galaxies at all these different wavelengths gives as a really good handle on the distribution of matter within a galaxy. Not just stars, but dust, gas clouds and the like. What we find is that galaxies really do have the majority of their mass in the center, and the motion of stars in the galaxy should be faster near the center than at the edge.

So if we have a good measurement of matter in a galaxy, and we have a good understanding of gravitational theory, why does our calculated result for stellar motion not match the observed result? Perhaps we don’t actually have as good of a handle on the matter of galaxy as we think. After all, we can only observe the light emitted from a galaxy, and even though we can observe galaxies at lots of different wavelengths, perhaps there is matter that isn’t giving off light. Maybe it is really cold dust or gas that doesn’t even give off much infrared, so we just aren’t seeing it.

The problem with this idea is two-fold. First, even “cold” matter will tend to give of some light, so for us to miss it it would likely need to be extremely cold and fairly diffuse gas. This leads to the second problem. If you look at a galaxy’s rotation curve and use gravitational theory to calculate how much “invisible” mass a galaxy has, what you find it that most of a galaxy’s mass would have to be of the “invisible” kind. Typically 80% – 90% of a galaxy’s mass would have to have to consist of this very cold gas or dust.

But if most of a galaxy consists of very cold “invisible” matter, we would see its effect. Cold gas absorbs certain wavelengths of light, and cold dust blocks or scatters certain wavelengths. If there were lots of gas and dust surrounding a galaxy, we would see absorption lines in the galaxy’s light, and scattering effects from the dust. We don’t see any such effect. Also, when a galaxy’s light is absorbed or scattered it would heat up the surrounding gas and dust, making it detectable at radio or infrared wavelengths, which again we don’t see. This simply cannot be the solution.

There are two other puzzling bits of evidence. The first is the observation of gravitational lensing by galaxies. One aspect of Einstein’s gravitational theory is that light can be deflected (or lensed) by the curvature of space near a massive object. This has been observed in starlight passing near our Sun, for example. We can see a similar deflection of light around galaxies. Since the amount of deflection or lensing depends on the mass of the galaxy, measuring the lensing allows us to determine the mass of the galaxy in a different way. What we find is that galactic mass as measured by gravitational lensing agrees with the galactic mass calculated by the motion of stars in the galaxy. According to gravitational theory, the mass of a typical galaxy is about 10x larger than the amount of mass we can observe.

A second part of the puzzle comes from the cosmic microwave background (CMB). The CMB is the first free light of the universe, formed when the matter of the universe finally cooled enough to form atoms about 380,000 years after the big bang. Since the CMB is from a time when atoms were forming, we can use it to calculate things like how many photons were produced for every baryon, known as the baryon-photon ratio. Things like protons and neutrons are baryons, so “normal” matter made up of atoms and molecules are sometimes known as baryonic matter.

The baryon-photon ratio we observe in the CMB tells us basically how much baryonic matter there is in the observable universe. What we find is that the amount of regular baryonic matter is a bit more than the amount of matter we observe in galaxies. This makes sense, because there is likely some cold matter between galaxies that we haven’t observed. This also means that 90% of a galaxy’s mass can’t simply be cold, regular, baryonic matter. Instead it would need to be some unknown type of non-baryonic matter. Something different from regular matter.

So direct observations of galaxies agree with observations of the cosmic microwave background on just how much (baryonic) matter there is in the universe. Observations of stellar motions in galaxies and of gravitational lensing tell us there should be more than 5 times that amount of matter in the universe. So we have one set of consistent evidence that disagrees with another set of consistent evidence by a factor of five. And therein lies the problem.

The clear next step is to reexamine our gravitational theory. Even though it is well supported by experimental evidence, the direct experiments have only been done within our solar system. Gravitational theory and astronomical observation agree perfectly within our solar system. The two only break down at galactic and cosmic scales. It seems reasonable to presume that gravity could be modified to account for galactic observations, just as Einstein modified Newton’s theory to account for observations Newton couldn’t predict.

We’ll look at that approach next time.