Matters of Gravity

NASA

Last time I talked about how motion is relative, and how relative motion affects our measurement of space and time. We ended with a very important aspect of physics: space and time are not absolute, but rather depend upon your point of view. Last time we saw how space and time can be effected by motion. Today we’ll look at what happens when gravity gets involved.

In our everyday lives, gravity is the pull of the Earth holding us to its surface. We think of it as a force (a push or pull) that acts on us and everything around us. But gravity behaves very different from other forces. Suppose I were to push a tennis ball and a bowling ball with equal force. The tennis ball would move much faster because it has less mass. However if I drop the tennis ball and bowling ball, they fall at exactly the same rate. Gravity pulls pulls them in such a way that their masses don’t matter. In fact, under gravity everything falls in the same way. It’s a property known as the equivalence principle. As a result, free fall feels exactly like no gravity at all. This is why astronauts on the international space station appear to be floating, when in fact they and the space station are all in free fall as they orbit the Earth.

By the principle of general relativity, free fall under gravity and the absence of gravity feel the same because they are the same. The idea seems ridiculous because we can see the space station orbit the Earth, so something must be pulling it. But remember that space and time are not absolute. The astronauts don’t feel any force, and their viewpoint is just as valid as ours. The solution to this paradox is to recognize that space and time are actually warped by the mass of the Earth. This warping of spacetime means that the path of the space station is bent, giving the appearance of a force acting on it. I’ve written about this in more detail before.

Because of this warping of space and time, time as measured on the Earth differs slightly from time as measured on the space station. This difference is very small. So small that if we ran a clock on Earth for a billion years the warping of time by Earth’s mass would only slow it by about a second. This difference only matters when you are making precise measurements, such as when using the GPS in your phone to find the nearest coffee shop.

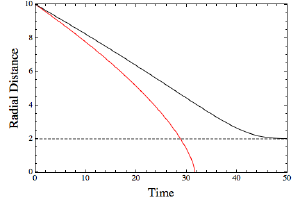
BK

For objects with much larger mass, the difference can becomes significant. As an example, consider the extreme case of a black hole. If you were to fall into a black hole, how long would it take you to reach the event horizon? Of course that depends on your point of view. In the figure I’ve plotted radial distance from the black hole as a function of time. For the red line, the time is that of the person falling into the black hole. For the black line, the time is that of a person watching the fall from a safe distance.

You can see that something interesting happens. For the person falling into the black hole, they reach the event horizon (indicated by the dotted line) at around the 30 mark. But from the outside observer’s view, they never reach the event horizon, but rather get ever closer at an ever slower pace. The outside observer sees the time of their falling friend get slower and slower as the black hole warps spacetime more and more. The falling explorer doesn’t experience that slowdown, and so reaches the event horizon in a finite time. Of course once our explorer crosses the event horizon they can never leave the black hole. Space and time have become so warped at the event horizon that it traps anything that crosses the line.

So what happens to light in all this? Both our outside observer and our free falling explorer still measure the same speed of light, but the difference in observed times means they disagree on a light’s color.

But we’ll look at that next time.