It Goes To Eleven

When we look around the universe we see the usual dimensions of length, width and depth as we move forward through the dimension of time at the rate of one second per second, and it all makes sense to us. However string theory (or more properly its offspring, M-theory) says that although we may seem to live in these four dimensions, we actually live in a universe of eleven dimensions. According to string theory the universe only appears 4-dimensional because, like Edwin Abbott’s flatlanders, we are trapped on a “plane” of four dimensions. The reason we are trapped is that all the strings we are made of — the electron, neutron, and proton strings — are open strings. The ends of these strings can’t flop around freely, but instead must be fixed to a membrane surface or “brane,” and are thus only able to move freely along this brane, specifically our usual four dimensions. Closed strings on the other hand can flow freely through higher-dimensional space. In string theory gravity is made of such strings, which would explain why gravity is so much weaker than other forces such as electromagnetism. The basic idea is that all the other forces are trapped on the brane, and are thus very concentrated, whereas gravity is spread throughout all eleven dimensions, and so seems much weaker in our regular space-time.

Still, other than mathematical elegance, why invoke higher dimensions in the first place? If we can’t see them, and physical objects can’t travel through them, then aren’t they superfluous? Not quite. It turns out that even though we can’t see higher dimensions directly, we might be able to detect them indirectly. To see how this might work, consider Newton’s theory of gravity in two dimensions.

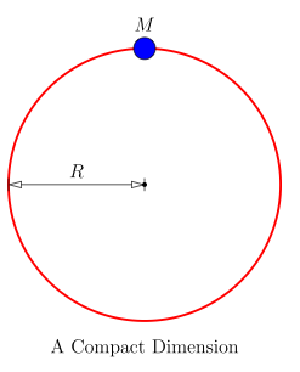
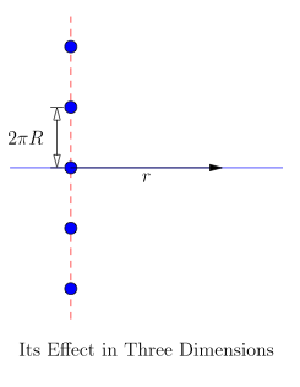
Brian Koberlein

For flatland physicists, who live on the surface of a 2-dimensional plane. They look around and see that gravity behaves as it should for two dimensions. In two dimensions gravity is proportional to the inverse of distance, not the inverse square of the distance. If their plane existed in three dimensions, their gravity would be an inverse square force just like ours. But suppose that in their universe, the third dimension isn’t flat and open as it is in our universe, but instead loops back on itself. If they could travel in this third dimension, they would find that after a short journey they would find themselves back where they started. Their universe would be 3-dimensional, just very thin. Put another way, if they assumed the third dimension was flat, they would see images of their universe over and over again. In the first figure, I’ve drawn a simple diagram of a closed dimension. In the second figure I’ve drawn how the mass and all of its images would appear to our flatland physicists.

Brian Koberlein

In such a universe, the force of gravity would be the usual inverse square form with one catch. All the images of a mass would have the same gravitational attraction as real masses. Since the third dimension is compact, to find the force of gravity from a mass we would have to add up the effect of an infinite number of masses spread evenly along the third dimension. The result is a bit complicated in general, but if the third dimension is really thin, then at the scale of our physicists the mass would look like a continuous line of mass. It turns out that the gravitational field from a long line of mass is proportional to the inverse of your distance from the line, just as if space were two dimensional. On the other hand, if our flatland physicists measured gravity on a small scale (on the order of the size of the extra dimension) they would see the effect of the discrete mass images. In other words, they would see that gravity it is almost 2-dimensional, but has a small extra term due to the small compact dimension. Our 2-dimensional physicists would see 2-dimensional gravity in their everyday world, but they might detect the third dimension if they take a closer look at gravity on either very large or very small scales.

We can apply the same idea to our universe, and what we find is that if all the “extra” dimensions are compact we would never notice their presence unless we look very closely at things small scale, such as the strength of gravity. So far, experiments to detect deviations from Newtonian gravity at small scales haven’t found any higher-dimensional effect. What they have shown is that either the universe consists of only the four dimensions we see around us, or else all dimensions beyond those four must be very small, no more than about 10 microns, roughly one-tenth the width of a human hair.