In a Relationship

One of the more interesting modern findings about galaxies is that most of them have black holes in their centers. We can’t observe these black holes directly, but we can see their effects through things such as high-energy jets streaming away from them. In many cases we can even get a measurement of their mass by observing the distribution of the speed of stars in a galaxy. I wrote about one such method about a year ago.

We’ve done this for quite a few spiral and elliptical galaxies, and it turns out there is a relationship between the distribution of stellar speeds in a galaxy and the mass of the central black hole. You can see this relation in the figure below from an article in the Astrophysical Journal.¹ Here the mass of the central black hole is plotted versus (a statistical measurement of ) the range of speeds.

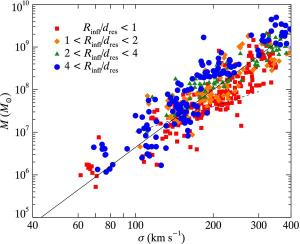Kayhan Gültekin, et al.

For this particular graph the measurement of stellar speed is precise enough that we can distinguish between a galaxy that has a black hole and one that doesn’t. This means we can use this relation to determine the mass of a black hole in galaxies where the stellar motion is less precisely known. If we know a black hole exists in a galaxy (say, by observing jets), we can use this relation to determine the mass of the black hole.

There is also a less precise measurement between the mass of a galactic black hole and the overall brightness of the galaxy. So even if we don’t have a measure of stellar speeds we can use a galaxies brightness to estimate the mass of a galaxy’s black hole.

Much of astronomy focuses on nailing down relationships like this one. We use the data we have to determine these relationships, then use those relationships to quantify things like black hole mass even when we can’t make a precise measurement. This means that even with a small amount of data we can determine quite a bit about a galaxy.