Hubble’s Constant

One of the more interesting astrophysical discoveries of the 20th century is the fact that the universe is expanding. The result was so unexpected that even Einstein discarded its prediction within general relativity. Einstein went so far as to introduce an extra constant in his equations specifically to prevent an expanding universe model. He would later call it his greatest blunder.

But how do we know the universe is actually expanding? For this we need to use the handy-dandy Doppler effect. You might remember that the observed color of light can be effected by the relative motion of its source. If a light source is moving toward us, the light we see is more bluish than we would expect (blue shifted). If a light source is moving away from us, the light is more reddish (red shifted). The faster the source is moving, the greater the shift.

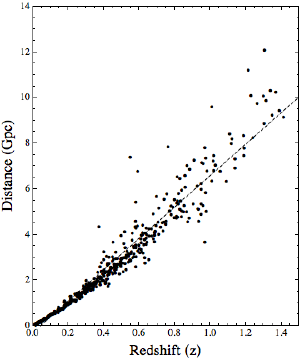
We have measured this color shift for lots of stars, galaxies and clusters. We’ve also determined their distances (exactly how will be a post for another day). If we plot a graph of the distance of galaxies and clusters versus their redshift we find something very interesting. I’ve plotted such a graph below, and you can see there is almost a linear relationship between distance and redshift.

Brian Koberlein

This means galaxies are not simply moving at random, as you would expect in a stable, uniform universe. Instead, the more distant the galaxy the faster it is moving away from us. This relation between distance and speed is the same in all directions, which means the universe seems to be expanding in all directions.

Since this relationship is linear, you can fit this data to a line. The slope of the line is known as the Hubble constant, named after Edwin Hubble, who was one of the first to observe this relationship. When I did a simple linear fit to the data (the dashed line), I got a Hubble constant of 68.79 km/s per megaparsec. This is in the range of the accepted value.

Of course if the universe is expanding, then it must have been smaller in the past. If we assume the universe expands at a constant rate, then we can trace its size back in time to a point where the universe would have zero volume. In other words, the universe has a finite age, and it began very small, very dense (and therefore very hot). We call that starting point the big bang. If you do the math, the age of the universe is simply the inverse of the Hubble constant. Given our value, this puts the age of the universe at about 14.5 billion years. More accurate calculations put the age at 13.75 billion years.