The Great Unknown

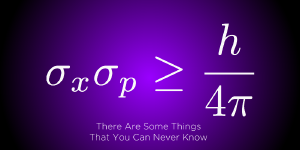Brian Koberlein

Last time I talked about how things like photons and electrons have a strange wave-particle duality. Related to this is the fact that there are limits to what you can know about quantum particles. To see how this works, let’s return to our baseball analogy. Suppose you were watching a game, and just after the ball was hit you wanted to determine where the ball will land. In principle you could measure the ball’s position and speed. Knowing its position and speed at a particular time you could then use Newton’s laws to predict where the ball will land. That’s because Newtonian mechanics is deterministic. If you know an object’s position and momentum (velocity and mass) and the forces acting on the object, then you know where it will be at any point in the future.

Of course in practice you can’t measure the ball’s position and speed exactly, so your measurements will have a bit of uncertainty. This means your prediction of where the ball lands will have a certain amount of uncertainty. It’s tempting to think of quantum particles in a similar way. They are so small that surely there will be some uncertainty in measuring them. However quantum uncertainty is completely different from the uncertainty of our baseball.

The key difference is that the baseball has a particular position and momentum. The uncertainty of our measurement of its position and momentum is a limitation of our knowledge of the ball. Quantum uncertainty is different. For example, with an electron there is an uncertainty to our measurement of its position and momentum, but that’s because the electron doesn’t have a precise position and momentum. If the electron had and exact position and momentum, then we could predict exactly where it would be in the future, just like the baseball. It would simply be a particle. But because of its wave characteristics, that is physically impossible.

This limitation is given by the equation below, which is known as the uncertainty principle. What it says is that the product of the uncertainty of position (x) and uncertainty of momentum (p) is no smaller than Planck’s constant divided by 4 pi. The more precisely you measure an object’s position, the more uncertain its momentum and vice versa.

This “fuzziness” factor leads to a number of strange effects, of which one is known as quantum tunneling. Suppose I put a plastic cup on a table, and put a ping pong ball beside the cup. Then suppose I asked you to put the ball in the cup without touching either the ball or the cup. You might suggest moving the table or some such “out of the box” trick, but I don’t allow that. You might then say what I ask is impossible, and for the cup and ball you’d be right.

But for quantum particles such a thing is possible. It would be as if the ball just happened to find itself inside the cup by chance. One moment the ball is outside the cup, and the next moment it is inside the cup. It is as if the ball “tunneled” into the wall of the cup, hence the name quantum tunneling. This effect is possible for quantum particles because of the uncertainty principle. If a quantum “ball and cup” are close to each other, the uncertainty principle means the ball could find itself inside the cup.

This quantum tunneling effect is necessary for the sun to be a star. The sun produces heat and light by fusing atoms. For example, hydrogen nuclei are slammed together so hard that they stick and produce helium atoms. The problem is that most of the hydrogen atoms in the sun’s core don’t have enough energy to stick together. To do that they have to overcome the repulsion of their positive charges, and they generally don’t have enough energy. To use our analogy, the ball is outside the cup, and it doesn’t have the energy climb up over the rim to get in the cup.

With quantum tunneling, however, the nuclei can cheat classical physics. They have enough energy to get relatively close to each other, and then they have a chance of tunneling through the remaining barrier to stick together. This window of opportunity is known as the Gamow peak, and it is a product of how much extra energy it needs and the odds of it quantum tunneling. Because of the Gamow peak, the nuclei in the sun can fuse despite the fact that they don’t have enough energy to fuse on their own. Without quantum tunneling, the sun wouldn’t be able to fuse nuclei in its core in any significant amount, which would mean it couldn’t be a star.

It’s important to emphasize that the equation below is physical law. The uncertainty principle isn’t a statement on the limitations of our knowledge a quantum particle. It is a recognition that quanta are not classical particles. They have an inherent fuzziness to them. This lies at the heart of quantum theory, and its full implications are still being explored.

But we do know that all the electrons and protons that make up the atoms in our bodies, all the starlight and sunlight and nuclear force gluons that drive the universe, all the building blocks of existence are all quanta. All this fuzzy, wavy, particle duality lies at the heart of everything, and it comes together to form a world that looks solid, and classical, and real. It is the very thing that allows the Sun to light our world. It is the very thing that allowed stellar fusion to create the oxygen in our lungs, the calcium in our bones, and the iron in our blood. It enables us to be.

Which in turn enables us to explore the great unknown.

Did you miss the beginning of the series? It all starts here.