Gravitational Redshift

I’ve been spending the afternoon book writing again. This time looking at another test of general relativity: gravitational redshift. As light leaves the surface of a star it must overcome the star’s gravitational attraction. By conservation of energy the light must lose energy to the gravitational potential of the star. Since the energy of a photon is inversely proportional to its wavelength, a loss of energy means the wavelength of the light must increase as it moves farther from the star. In other words, the light is gravitationally redshifted.

For a star like our sun, this redshift is rather small. Our sun is not massive enough or dense enough to have a really large gravitational redshift. For white dwarfs, however, the redshift can be much larger, and we’ve measured this redshift for several white dwarfs.

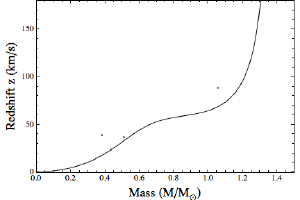
The relation between the mass of a white dwarf and its radius is rather complicated, as it depends on quantum statistics. But once you calculate the mass-radius relation, calculating the expected redshift is easy. Then we can compare the expected redshift of our white dwarf model with the observed redshift of various white dwarfs.

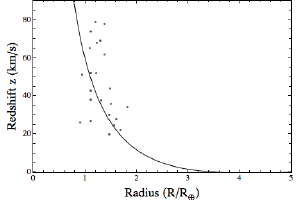BK

BK

In the figures above I’ve done just that. The first figure compares the theoretical model against the few white dwarfs for which we know their mass. The second figure compares theory to white dwarfs with known radii. As you can see there is a general agreement with our model, but the correlation isn’t overly strong. It seems we have more to learn about white dwarfs.