Equations of State

Imagine a star twice as massive as the Sun, compressed to the size of a city. All that matter squeezed into a sphere about 15 miles wide. Such an object is known as a neutron star. The matter of a neutron star is so dense and its gravity is so strong that atoms cannot support themselves. Instead they collapse, with the electrons being squeezed into the nuclei until what remains is a mass of neutrons. Hence the name.

The exact structure of a neutron star is still a bit of a mystery. At a broad level, they are just large balls of neutrons, but they have strong gravitational and magnetic fields that can affect their structure, and then there are the neutrons themselves. How do we understand “stuff” made out of neutrons, when what we see around us are made of atoms? The key is to determine its equation of state.

The equation of state of a material determines its bulk properties. If you’ve had a chemistry class you are likely familiar with the ideal gas law, which describes how the pressure, temperature and volume of a gas are related. The ideal gas law is an equation of state for a simple gas.

We have observed the gas law experimentally, but we can also derive its properties mathematically using kinetic theory. Since a gas tends to be relatively low density, we can treat the atoms or molecules almost as billiard balls that bounce against each other. Modelling a gas in this way gives us the ideal gas law.

Equations of state are the key to understanding stars and the like, because stars are a balance between the weight of the star’s matter and its pressure. Knowing the equation of state for a star’s material means we can calculate things such as size and temperature. Likewise if we know a stars size and temperature we can gain an understanding of the equation of state.

Neutrons (and electrons) obey a different equation of state from that of a simple gas. It is derived from Fermi-Dirac statistics, which takes into account what is known as quantum degeneracy pressure. If you are familiar with the Pauli exclusion principle, which states that no two electrons can occupy the same state, then you are familiar with one example of degeneracy pressure. The basic idea of degeneracy pressure is that there is a minimum volume into which you can squeeze a neutron. Beyond that limit the degeneracy pressure gets too large for you to overcome.

This doesn’t mean you can never overcome that pressure. You can overcome the degeneracy pressure if you have enough mass. Based on the neutron equation of state that limit is a bit more than 3 solar masses. Anything bigger than that, and the neutron star is so massive it collapses into a black hole. A similar thing occurs with white dwarfs. In a white dwarf star the weight of its mass is balanced by the degeneracy pressure of the electrons. As long as the white dwarf is less than 1.4 solar masses (the Chandrasekhar limit), then everything is fine. But if the white dwarf has more mass, then it will collapse into a neutron star.

There is, however, one important difference. Electrons are elementary particles, which means they aren’t made of anything smaller. So when a white dwarf is more massive than the Chandrasekhar limit it can’t do anything but collapse into a neutron star. But neutrons aren’t elementary particles. They are made up of a trio of quarks. So when if the mass of a neutron star is close to the neutron limit, then it might not collapse into a black hole. It might collapse into a quark star.

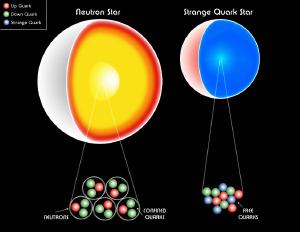CXC/M. Weiss

In a quark star, instead of being clumped into neutrons the quarks would move freely, making the star a mass of quarks, as you can see in the figure. Of course this means that a quark star needs an entirely different equation of state. This is further complicated by the fact that the interior of quark stars would have so much heat and energy that some of the neutron quarks (up and down quarks) could transform into strange quarks. (Not strange in that they are weird, but strange because they are named strange quarks). The interior of a quark star could then be strange matter, and we don’t know exactly what it’s equation of state would be.

We don’t have a solid theoretical understanding of quark matter, but most models predict that quark stars would be slightly smaller than neutron stars. The one catch is that the largest quark stars could be as large as the smallest neutron stars, so it might be difficult to distinguish them. There have been a few observations of stars that might be quark stars, but so far there are no confirmed quark stars.

Then again it might be the case that quark stars are unstable. This would mean that large neutron stars might enter a short quark star period before collapsing into a black hole, but there would never be a long-lived quark star. We aren’t really sure at this point.

In the end it will all come down to their equation of state.