Coin Toss

Suppose you were given one million dollar coins. Sure, you could spend it on something frivolous like paying off your house or your college loan, but could also use those million coins to play a game related to quantum physics. The rules of this game are simple. Each round every coin gets tossed once. Any coin that lands on tails gets to move to the next round. Any coin that lands on heads is eliminated from the game. Keep playing until you run out of coins. I would call this game Half-Life, but since that’s already been taken, I’ll call it Coin Toss.

Assuming all of the coins are fair, each coin has a 50% chance of making the second round. Any coin that makes it to the second round has a 50% chance of making it to the third and so on. Even if a coin makes it to the 10th round (meaning it landed on tails ten times in a row) it still has only a 50% chance of making it to round 11. The fact that a particular coin has survived all the past rounds doesn’t make it any more or less likely to land on tails again. Each coin is completely random, and we have no idea when any particular coin might land on heads.

On the whole, however, we can say some things about the outcome. While it is (remotely) possible that all the coins survive the first round, that isn’t very likely. We can be pretty confident that about 500,000 of the coins will make it to the second round, about 250,000 would make it to the third, and so on. It is very possible that 1 or 2 coins will survive to round 19. Even though we can’t predict the outcome of an individual coin, we can predict the collective outcome with a high degree of certainty.

Our confidence in the outcome is high enough that if we know the rate at which each round was played (say once a day, or once a week) we can count the number of coins still in play to determine how long ago the game began. We don’t have to know the exact outcome because we know the game and the rate at which it plays.

In scientific terms we call this radiometric dating. Some elements are radioactive isotopes. They are unstable, which means they can decay into other elements over time. We can’t determine when a particular radioactive atom might decay, but we do know the half-life of radioactive isotopes. Basically, the half-life is the rate at which they play the game. Different isotopes have different half-lives, but they all play the same game. With each half-life a particular isotope has a 50% chance of still being in the game.

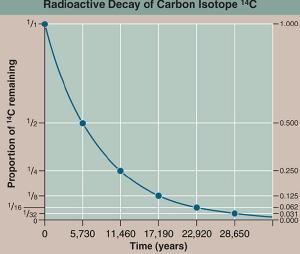
yellowtang.org

Perhaps the most famous isotope is carbon-14. This isotope is generated at a fairly constant rate when cosmic rays strike nitrogen atoms in the upper atmosphere. Living things take in new carbon at a fairly regular pace, so they all have a fairly constant fraction of carbon-14. When things die they stop taking in new carbon, and the fraction of carbon-14 decays with a half-life of about 6,000 years. So we can measure the fraction of carbon-14 in something dead to determine when it was alive.

Of course this dating method gets less accurate as more and more rounds are played, and this means there’s an effective limit to how far back we can date something with a particular isotope. For carbon-14 that’s about 60,000 years (or about 10 rounds of the game). Other isotopes, such as uranium-lead dating can determine the age of rocks more than two billion years old (give or take a few million years).

Radiometric dating can even tell us something about supernovas, but that’s a story for another time.