Close Encounters

The average distance between stars in our solar neighborhood is about one parsec, or just under 4 light years. While this is a massive distance on our scale, from a star’s perspective it isn’t overly large. Since stars are always moving relative to each other, there are bound to have been “close encounters” with other stars over the roughly 5 billion year history of our solar system.

By close I mean distances on the order of 1/20 of a parsec or less. The radius of our solar system is about 1/5000 of a parsec, so even such close encounters have no chance of colliding with a planet. Still, the close approach of a star would gravitationally pull on the planets ever so slightly, which means the planets would shift in their orbits by a tiny amount. Kind of like the flutter of a butterfly’s wings makes a tiny bit of breeze.

This raises an interesting question about the stability of our solar system. Would it be possible for a small tug from a visiting star to throw planets out of their orbits over millions of years. Is it possible to have a planetary “butterfly effect”?

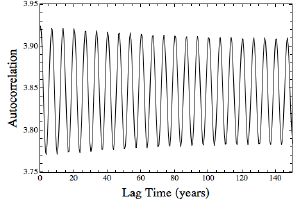
Brian Koberlein

One way to test this would be to run simulations of the solar system over millions of years, but unless you want to pay for time on a supercomputer cluster that isn’t very practical. Another way is to run a simulation over a few hundred years, and then look at how statistically similar the motion remains over time. In mathematics, this measure of similarity is known as a correlation function. In the figure here I’ve plotted the correlation function for Mercury over about a century. You can see there is a periodic oscillation (which is due to the precession of Mercury’s orbit over time) but you can also see that the overall amplitude of the oscillation is decreasing over time. This basically means that Mercury’s orbit is slightly losing its consistency over time.

If you look at the rate of that decay, you can calculate what is known as the correlation time. This is a measure of how long (based on your model) you could expect the orbit to be stable. In the case of Mercury this turns out to be about 30 million years. This does not mean that Mercury will tumble out of its orbit after that time, but rather than its orbit will remain largely unchanged for at least that long.

Brian Koberlein

If you calculate the correlation time for all the planets, you get times on the order of tens of millions to billions of years, which means our solar system seems to be pretty stable. If you do the same calculation for Pluto, however, you get a time of only about 10,000 years. The orbit of Pluto is not nearly as stable as those of the classical planets.

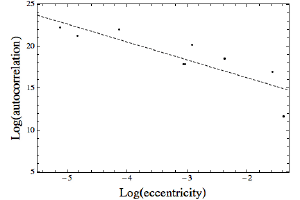
Although we only have about a dozen planets to work with (if you count Pluto, Ceres, etc.), you can look at some of the factors that make a planet more or less stable. For example in the second figure I plotted the correlation time of the planets with the eccentricity of their orbits (how elliptical they are). You can see that the more elliptical the orbit, the less stable the orbit appears to be.

Not unexpectedly, it turns out that the most stable planets are ones that are reasonably massive, with fairly circular orbits close to their star. Small mass planets far from their star in elliptical orbits are much less stable. This means that when we look for planets around other stars we would expect to find lots of large planets orbiting in circular orbits near their star, which is exactly what we are finding.