Chandrasekhar Limit

The bulk of my grading for the term is done, so I finally have time to write about astrophysics. Last time I talked about a simple model for a star: an ideal gas held together by gravity. As we saw, the result wasn’t particularly effective. Of course that’s perfectly understandable, since we ignored the fusion in the core, radiation pressure, convection, etc., etc. Given all that we ignored, it’s a wonder our model worked at all.

But sometimes a rough model can be dusted off and used in ways we didn’t expect. Our simple stellar model wasn’t great for a regular main-sequence star that’s fusing and radiating, but it would be a decent model for a star that isn’t fusing and isn’t radiating much. It turns out there is exactly such a star, known as a degenerate star. It’s commonly known as a white dwarf.

A white dwarf forms when a star such as our sun has fused all the elements it can, and has therefore “run out of fuel.” Larger stars can explode into supernova, but stars like our sun simply swell into a red giant for a while, then gradually cool down. With no more fusing core, the old star is basically just a hydrostatic mass. The key difference is that the density is so high it isn’t a regular ball of gas, but rather a gas of plasma. All the ions and free electrons act somewhat like a regular gas, but with one big exception: the electrons and ions obey the Pauli exclusion principle.

In broad terms the Pauli exclusion principle means that the electrons can’t occupy the same state. It is kind of like musical chairs where everyone jostles each other to find a seat, and two people can’t share the same seat. The exclusion principle also applies to the ions, but it turns out that the electrons need bigger chairs, so it’s the electrons we most have to worry about. As a result of the exclusion principle the electrons exert a degeneracy pressure to keep all the other electrons out of their chair. You can therefore treat the electrons as a simple gas with a pressure due to the exclusion principle. So to model a white dwarf, we just need gravity and the equation of state (a description of the pressure) for our electron gas. Which brings us back to our simple stellar model. We have a different pressure equation, but our white dwarf is in hydrostatic equilibrium, so our simple model is now pretty reasonable.

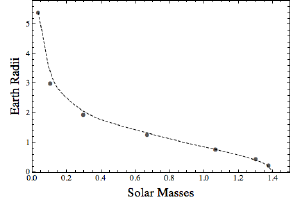
BK

So let’s use the same model as last time, but with electron degeneracy pressure instead of ideal gas pressure. In the figure I’ve plotted the radius of star for a given mass. Calculating the radius means I had to calculate the pressure and density functions first, then integrate those functions to determine the radius. It is a pretty intense calculation for a desktop, so I’ve only calculated a few examples (the dots on the figure). There are enough points to give a function fit, which I’ve also plotted.

As the mass of a white dwarf increases, the radius decreases. This is exactly what we would expect, since more mass means stronger gravity, which means all those degenerate electrons are squeezed harder. But when the mass reaches about 1.4 solar masses, the electrons are squeezed so tightly that the resulting radius is zero. At this limit the electron pressure can’t withstand gravity. This limit is known as the Chandrasekhar limit (named after its discoverer). Above this limit and the electrons are squeezed into the protons in the ions, leaving a massive ball of neutrons known as a neutron star. Okay, it isn’t quite that simple, but you get the idea.

So this time our simple model is really useful. It tells us that white dwarfs have a mass limit of about 1.4 solar masses, which is exactly what we observe.