By the Numbers

The orbits of three of the moons of Jupiter (Io, Europa and Ganymede) have an interesting pattern. For every time Ganymede orbits Jupiter, Europa orbits twice, and Io orbits four times. In other words, the periods of their orbits follow the ratio of 1:2:4. This is known as an orbital resonance, and it occurs a number of times in our solar system. Saturn’s moons of Hyperion and Titan have a 3:4 resonance, and Pluto and Neptune a 2:3.

Resonance orbits occur because their effect builds over time. For example, if Europa’s orbit were slightly less than twice as long as Io’s, then they would almost line up at each orbit. Their gravitational pull on each other would tend to slow down one slightly and speed up the other, until their orbits matched more closely. When the moons are in resonance, their gravitational pulls reinforce their orbits, making them more stable. In the case of Jupiter’s moons, this is known as a Laplace resonance.

Resonances can also work to destabilize orbits. This can be seen in the asteroid belt. The orbital periods of the asteroids in the belt tend to be clumped into groups, with gaps (known as Kirkwood gaps) at resonances of 3:1, 5:2, 7:3 and 2:1 with Jupiter. Since Jupiter is so massive compared to the asteroids, the asteroids are quickly perturbed away from these resonant orbits, into either a larger or smaller orbit.

Computer models of orbital systems show similar resonances, so it has long been thought that such resonances would occur in any planetary system. This should particularly be true for planets of similar mass orbiting close to their star (analogous to the moons of Jupiter).

Konstantin Batygin, Alessandro Morbidelli

Recently a research team looked at the orbits of exoplanetary systems.¹ That is, stars with at least three known planets with well defined orbits. There are about 40 such systems currently known. The team analyzed the orbits of these systems, and found that a third of them had planets in resonant orbits (2:1, 3:2, 4:3, etc.). This is much higher than one would expect if the planets were just randomly distributed, which indicates that the resonances do play a role in the formation of solar systems.

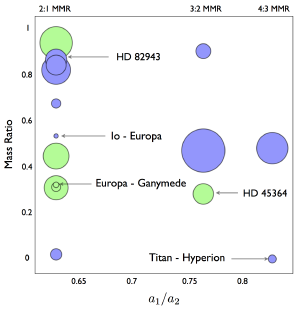
You can see these resonances in the figure above,² which plots their orbit ratios in comparison to their mass ratios. One of the things you’ll notice is that the resonances don’t seem to depend on the relative masses of the planets, which agrees with computer simulations that have been done.

So it seems some planets really do go by the numbers.