Astral Projection

You can’t make an accurate flat map of the entire Earth. Since the Earth is not flat, a map is typically a projection of the Earth onto a flat surface. As a result, the shapes of the continents are distorted. Perhaps the most famous example of such a projection map is the Mercator projection, which distorts the size of polar regions over equatorial ones. As a result, Greenland looks as big as Africa when in fact Africa is 14 times larger. Mercator is useful if you are navigating the oceans, since navigations lines remain straight on a Mercator map, but it doesn’t preserve the areas of different continents.

There are several ways to make a projection map that preserves area, one of which is the Mollweide projection, seen in the bottom of the figure below. In this map you can see that Greenland really is much smaller than Africa. One disadvantage of a Mollweide map is that areas near the edges are very distorted.

A compromise is to require that area be reasonably proportional, but not that it be exactly accurate. This means you can relax the area requirement a bit near the edges so that things are not so distorted. One of these compromise projections is known as the Aitoff projection, seen in the top of the figure below. This projection preserves distance along the equator and pole to pole at a 2 to 1 ratio. It is the same shape as Mollweide, but doesn’t have as much distortion of shape.

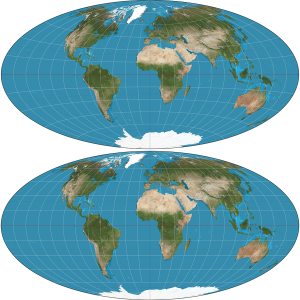Wikipedia

So how does all this relate to astrophysics? If you want to make a map of the sky, you have the same problem. The Celestial Sphere must be mapped onto a flat surface. Different types of projections are used to display objects in the sky. The Aitoff projection is often used for astronomical maps since it is a good compromise projection. However the famous cosmic background maps are shown as Mollweide projections.

Of course this does lead to a problem if you happen to be writing an astrophysics book. If you look at an Aitoff and Mollweide projection they look very similar. If you have a sky map it is even more difficult to tell them apart. The two are so similar that some publications and websites say a map is an Aitoff projection when it is a Mollweide projection. Other maps are presented without stating the type of projection. If you aren’t careful, you can assume one projection when it is actually the other, and it will screw up your data analysis in a particular chapter.

When the copy edits come back you get to rewrite that section while kicking yourself for not catching your mistake earlier.