Across the 8th Dimension

A few years ago a research team measured the force of gravity over very small distances.¹ Their result places very stringent constraints on the space-time structure of our universe. Either the universe consists of only the four dimensions we see around us, or else all dimensions beyond those four must be very small, no more than about 10 microns, roughly one-tenth the width of a human hair. What, you might ask, does proving Newton right (yet again!) have to do with hyperdimensional physics? Quite a lot, it turns out.

We look around and see the usual dimensions of length, width and depth as we move forward through the dimension of time at the rate of one second per second, and it all makes sense to us. However string theory (or more properly its offspring, M-theory) says that although we may seem to live in these four dimensions, we actually live in a universe of eleven dimensions. According to string theory the universe only appears 4-dimensional because, like Abbott’s flatlanders, we are trapped on a “plane” of four dimensions.

The reason we are trapped is that all the strings we are made of – the electron neutron and proton strings – are open strings. The ends of these strings can’t flop around freely, but instead must be fixed to a membrane surface or “brane”, and are thus only able to move freely along this brane, specifically our usual four dimensions. Closed strings on the other hand can flow freely through higher-dimensional space. In string theory gravity is made of such strings, which would explain why gravity is so much weaker than other forces such as electromagnetism. The basic idea is that all the other forces are trapped on the brane, and are thus very concentrated, whereas gravity is spread throughout all eleven dimensions, and so seems much weaker in our regular space-time.

Still, other than mathematical elegance, why invoke higher dimensions in the first place? If we can’t see them, and physical objects can’t travel through them, then aren’t they superfluous? Not quite. It turns out that even though we can’t see higher dimensions directly, might be able to detect them indirectly.

To see how this might work, consider Newton’s theory of gravity. In three spatial dimensions, Newtonian gravity near a mass is inversely proportional to the square of the distance from the mass. In two spatial dimensions, gravity is inversely dependent on the distance. In general, the number of spatial dimensions determines the power (1, 2, 3) at which gravity is inversely dependent.

It would seem we have a simple rule of observation. By determining the value of of that power for gravity, we can determine the dimension of space. Since we observe that power is 2 (inverse-squared), we must live in a universe of 3 spatial dimensions. However, this only works if space is simple, flat and infinite. If some of the dimensions are compact – that is they loop back on themselves rather than spreading out forever – then all bets are off.

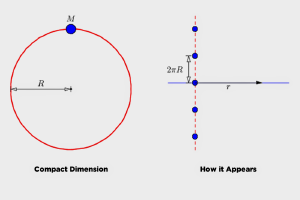
Consider our flatland physicists, who live on the surface of a 2-dimensional plane. They look around and see that gravity behaves as it should for two dimensions, and thus they observe the power of gravity is 1 (inverse linear). If their plane existed in three dimensions, their gravity would be like ours.

But suppose that in their universe, the third dimension isn’t flat and open as it is in our universe, but instead loops back on itself. If they could travel in this third dimension, they would find that after a short journey they would find themselves back where they started. Their universe would be 3-dimensional, just very thin. Put another way, if they assumed the third dimension was flat, they would see images of their universe over and over again.

Brian Koberlein

In such a universe, the force of gravity would be inverse-square, but they would only notice it at small distances. Since the third dimension is compact, all the images of a mass would have the same gravitational attraction as real masses. This is complicated in general, but basically if the size of the compact dimension is really large compared with their distance from the mass, then the result is standard Newtonian gravity in three dimensions. On the other hand, compact dimension is very, very small, then it is almost 2-dimensional gravity.

Our 2-dimensional physicists would see 2-dimensional gravity in their everyday world, but they might detect the third dimension if they take a closer look at gravity on either very large or very small scales. We can apply the same idea to our universe, and what we find is that if all the “extra” dimensions are compact we would never notice their presence unless we look very closely at things small scale, such as the strength of gravity.

As this latest experiment shows, we seem to live in a four-dimensional world. Either that or the “higher dimensions” are smaller than some string models presumed.