Weight for It

Warner Bros.

In an earlier post I wrote about how light moves at a single universal speed. Not only has this been well observed experimentally, it forms the foundation for the theories of special and general relativity, which are also well supported by experiment. Often, relativity is summarized as “nothing can travel faster than light.” Which raises the interesting question, what about gravity?

At a basic level gravity is the mutual attraction that exists between masses. In Newton’s gravitational theory, gravity is a force between masses, and it acts instantly across any distance. At Newton’s time, there was no reason to suspect a cosmic speed limit, and so Newton assumed gravitational forces must act instantly.

By the early 1800s, Pierre-Simon Laplace had developed a way to describe Newtonian gravity as a gravitational field around a mass. Other masses would sense this field as a force acting upon them. The result is the same as Newton’s “force at a distance” approach if gravity acts instantly, but Laplace wondered what would happen if gravitational fields took time to propagate. If that were the case, then the gravitational force a planet experiences would be where the Sun was, not where it is. If gravity travelled at the speed of light, the Earth would try to orbit the point where the Sun was 8.3 minutes ago. As a result, planetary orbits wouldn’t approximate Kepler’s laws, and they would become unstable over time. Since planetary orbits do approximate Kepler’s laws and are stable, Laplace’s result was used as an argument against finite-speed gravitational models such as Le Sage’s shadow gravity model, and the idea that the Sun and planets were electrically or magnetically charged.

In Einstein’s theory of gravity, the gravitational forces we observe are due to the warping of space and time by masses. Thus the Sun bends spacetime near it, and the planets traverse their curved orbital paths as a result. As strange as this idea might seem, it has been verified through a range of tests. Most of the predictions of general relativity have been verified, including gravitational lensing, gravitational redshift, orbital precession, and the Shapiro time delay. One of the few predictions that hasn’t been observed directly is gravitational waves.

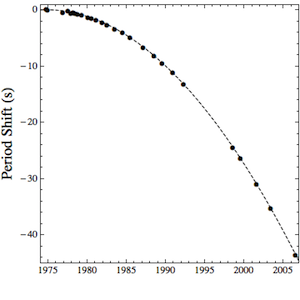
Brian Koberlein

According to theory, for example, when two large masses such as neutron stars orbit each other, they should produce gravitational waves that radiate away from them. These gravitational waves should travel at the speed of light. There have been experimental attempts to detect such gravitational waves, but they have been unsuccessful so far. We have, however, found indirect evidence of gravitational waves. By observing a binary pulsar, we have observed its orbit decay slightly over time. This orbital decay is due to the fact that gravitational waves carry energy away from the system. The rate of this decay matches the prediction of general relativity perfectly. Since this rate of decay depends crucially on the speed of gravitational waves, this is also indirect confirmation that gravitational waves move at the speed of light.

But if gravity moves at the speed of light, doesn’t that mean that planetary orbits should be unstable? Actually, no. When Laplace studied finite-speed gravity, he considered only the effect of the speed of gravity, which is what leads to his result, but in special and general relativity, the finite speed of light leads to other effects, such as time dilation due to relative motion, and the apparent change of mass due to relative motion. Mathematically these effects arise because of a property known as Poincaré invariance. Because of this invariance, the time delay of gravity and the velocity dependent effects of time and mass cancel out, so that effectively masses are attracted to where a mass is. This canceling effect means that for orbital motion it is as if gravity acts instantly.

Such a perfect cancellation might seem strangely convenient, but it occurs only if light and gravity have the same speed. Of course both special and general relativity were built upon that experimental fact, so it’s no coincidence that everything evens out.

As best we can tell, gravity really does move at the speed of light.