Sounding Older

Max Planck Institute

A few days ago I wrote about a planetary system discovered around an ancient star. I noted that the age of this star had been determined using asteroseismology, but how exactly does that work? What do sonic vibrations in a star have to do with its age?

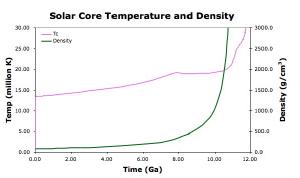
Brian E. Martin

It all has to do with the way stars age.¹ A main sequence star such as the Sun spends most of its life in a balance between its gravitational weight trying to crush the star, and the fusion driven pressure of its core opposing that weight. While the Sun and other stars are mostly composed hydrogen, the nuclear interactions in their cores gradually transform some of that hydrogen into helium and other elements. This means that the density of a star increases with age. Since a more dense star allows gravity to squeeze it more strongly, the pressure and temperature also increase over time. Given the rate at which stars give off light energy, we can determine the rate at which fusion occurs, and thus determine how the density, pressure and temperature of a star will change over billions of years.

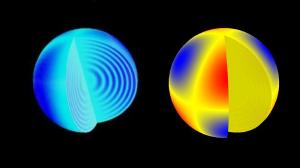
This is where asteroseismology comes in. The behavior of sound waves in a medium depends upon things like pressure, temperature, and density. By observing the oscillations of a star due to the sonic waves moving through it, we can categorize them into different modes. One type known as p-mode depend upon the speed of sound in the star, from which we can determine pressure and density. Another known as f-mode depends upon the surface gravity of a star. Given the density and surface gravity we can calculate the star’s mass. From these different modes we can determine where a star is along its evolutionary history, and thus determine its age.

There are other ways to determine the age of a star, and it is always useful to compare different methods for better accuracy, but one can get a fairly reasonable answer from stellar sounds alone.