It’s Only a Model

Johannes Kepler

When Johannes Kepler proposed a new model of the solar system in the early 1600s, it was a revolutionary idea. The model addressed many of the problems with earlier circular-orbit models, and greatly simplified the calculation of planetary motions. Still, the model was so radical that it wasn’t fully accepted until Newton was able to derive the model from his law of universal gravitation. What made Kepler’s model so powerful is that is required only three simple rules, which we now call Kepler’s laws.

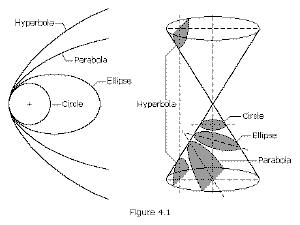
Wikipedia

The first law is that planetary bodies move in ellipses with the Sun at one focus. Kepler was only concerned with planets, but when Newton derived the law he found that it could be more generally stated that solar system bodies followed conic sections. A conic section can be found by taking a circular cone and slicing it at different angles. Slice it horizontally and you get a circle. Slice at a slight angle and you get an ellipse. Slicing ever steeper you eventually get a parabola, and then a hyperbola. Planets move in nearly circular ellipses, while comets can move in parabolas (or nearly parabolic ellipses) and even hyperbolas.

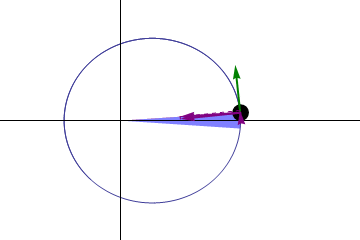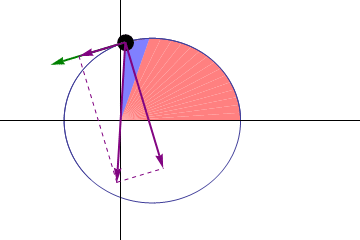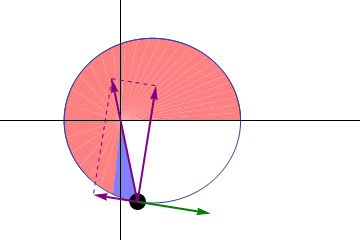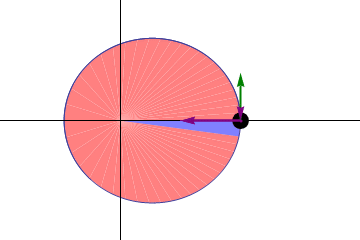
Wikipedia

While the first law determines the shape of an orbit, the second law described how planets move along their orbit. Expressed geometrically, it states that a line from the Sun to a planet will sweep out an area at a constant rate. This means that when a planet is farther from the Sun (and thus a longer line) it moves more slowly, and when close to the Sun it moves more quickly. While this seems like an awkward rule, it was actually quite useful for astronomers at the time who used geometry to calculate planetary motion. We now know that this law is an expression of a quantity known as angular momentum, and simply states that the angular momentum of an orbiting body is constant.

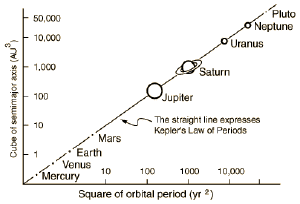
Wikipedia

The first two laws are sufficient to calculate the motion of planets, so it was another decade before Kepler came up with his third law. This one relates the orbital motions of different planets to each other, and a kind of unifying principle of planetary motion. What it says is that if you square the orbital period of a planet (in Earth years) and cube the semi-major axis of its orbit (in astronomical units) then you will find that they will equal each other. All planets follow this relation, so it is a basic principle of orbital motion. We now know that they just happen to be equal to each other because of the choice of units. More generally, the two quantities are proportional to each other, and the constant of proportionality depends upon the mass of the central body (in this case the Sun). The fact that all planets follow the same constant is due to the universal law of gravity.

The interesting thing about Kepler’s laws is that by the time they were confirmed by Newtonian gravity, it was also shown that they were only an ideal approximation. In the real solar system, gravitational interactions between planets cause them to deviate slightly from Kepler’s laws. In the end, Kepler’s laws are only a model, and not a true physical law. But despite its problems, it is remarkably accurate for such a simple model. Even though we’ve moved on with Newton’s gravity, and later Einstein’s general relativity, we still use Kepler’s laws as a basic calculation. It’s good enough to be used to calculate orbits of exoplanets, the masses of binary stars, and even the mass of the black hole in the center of our galaxy. It’s a great example of how simple models are extremely useful, even when they aren’t perfect.