Let There Be Rock

Gerd Altmann, via Pixabay

In 1905 Albert Einstein wrote four groundbreaking papers on quantum theory and relativity. It became known as Einstein’s annus mirabilis or wonderous year. One was on brownian motion, one earned him the Nobel prize in 1921, and one outlined the foundations of special relativity. But it’s Einstein’s last 1905 paper that is the most unexpected.¹

The paper is just two pages long, and it outlines how special relativity might explain a strange aspect of radioactive decay. As Marie Curie most famously demonstrated, some materials such as radium salts can emit particles with much more energy than is possible from simple chemistry. Einstein’s little paper speculated about the excess energy might be balanced by a loss of mass of the nuclear particles. This idea eventually led to Einstein’s most famous equation, E = mc².

1904, author unknown

This equation is often taken to mean that matter and energy are two sides of the same coin. It actually means that the apparent mass and energy of an object depend upon the relative motion of an observer, and because of this, the two are intertwined, similar to the connection between space and time. But one consequence of this relation is that under the right circumstances objects should be able to produce energy via a loss of mass.

We now know this is exactly what happens in radioactive decay. The effect is also how stars create energy in their cores via nuclear fusion. Of course, if matter can become energy, then it should also be possible for energy to become matter. That trick’s a bit more difficult, and it took particle accelerators to pull it off. These days we do this all the time. Accelerate particles to nearly the speed of light and slam them together. The large apparent mass of the particles releases tremendous energy, and some of that energy changes back into particles. All of modern particle physics can trace its history to Einstein’s two-page paper.

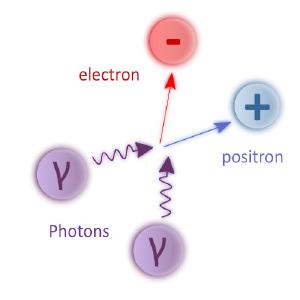
Mathieu Michel Lobet

But the laws of physics don’t just say you can create energy from matter and vice versa, it places specific constraints on the nature of the created matter and energy. One of the simplest examples of this is electron-positron annihilation. This happens when an electron collides with its antimatter twin. The two particles have the same mass, but opposite charge, so when they collide they produce two high-energy photons. The mass of the electron and positron are transformed entirely into energy. This experiment was first proposed in the 1930s, but it wasn’t done until 1970.²

If you can convert matter entirely into energy, you should be able to do the reverse. It’s known as the Breit–Wheeler process and involves colliding two photons to create an electron-positron pair.³ While we have used light to create matter several times, converting two photons directly into matter is very difficult. But a recent experiment shows it can be done.⁴

The team used data from the Relativistic Heavy Ion Collider (RHIC) and looked at more than 6,000 events that created electron-positron pairs. They didn’t simply beam two lasers at each other but instead used high-energy particle collisions to create intense bursts of photons. In some cases, these photons collided to create an electron-positron pair. From the data, they could show when a pair was created directly from light.

Since these pair productions occurred in the intense magnetic field the team also demonstrated another interesting effect known as vacuum birefringence. Normal birefringence occurs when light is split into two beams of different polarization. This effect occurs naturally in materials such as Iceland spar. With vacuum birefringence, light passing through an intense magnetic field is split into two polarizations, with each polarization taking a slightly different path. It’s an amazing effect if you think about it because it means you can change the path of light in a vacuum, using only a magnetic field. Vacuum birefringence has been observed in the light coming from a neutron star, but this is the first time it’s been observed in the lab.