A Lack of Balance

Claire David / CERN

Yesterday I wrote about the difficulty in understanding black holes. The heart of this difficulty lies in trying to understand how two radically different physical models (general relativity and quantum mechanics) might integrate into a single, unified model. Two major approaches to this problem are loop quantum gravity and string theory.

Loop quantum gravity (LQG) takes the approach of trying to bring space and time into a quantum framework. It gets its name from the fact that solutions to quantized gravity equations are known as loops (or graphs). One consequence of this model is that spacetime has a granularity to it. The granularity only appears at the Planck length scale. A Planck length is extraordinarily small. If you compared the size of a period in this post to the size of the observable universe, it is about the same as the size of a Planck length to the size of the period. On any normal scale this granularity would average out and look like a continuum, just as general relativity predicts. At high energies and small scales, the quantum aspects come into play. The problems with black hole singularities could be solved by loop quantum gravity.

String theory (or its generalization M-theory) takes a different approach. In string theory elementary particles such as quarks and electrons are not point particles, but rather loops (strings) of energy where the modes of oscillation can determine the properties of the particles. String theory has several advantages, such as an inherent connection between quantum theory and gravity. Some models require more dimensions than the 3 of space and 1 of time we see around us, but more complex versions can be formulated within the 4-dimensional framework we observe.

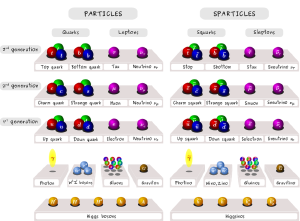
Both of these approaches hold promise in solving the quantum-GR problem, but both are also based upon a concept known as supersymmetry. In particle physics we have found that elementary particles can be divided into two main groups: fermions such as electrons and quarks, and bosons such as photons and gluons. This distinction is based upon an inherent property of particles known as spin, but basically fermions constitute matter, and bosons are the quanta of the fields through which matter interacts. Supersymmetry proposes that each elementary particle as a supersymmetric pair of the opposite type. Thus, for the fermionic electron, there is a bosonic selectron. For the bosonic photon, there is a fermionic photino, etc.

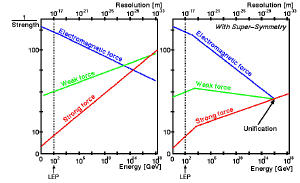
CERN

This grand symmetry between particles allows both LQG and string theory to unify gravity and quantum mechanics. Supersymmetry also solves a problem in the standard model of particle physics. In the standard model, three fundamental forces (electromagnetic, strong and weak) don’t quite unify at a common temperature (known hierarchy problem), but with supersymmetry they do. Thus supersymmetry not only provides a connection between quantum theory and gravity, it also provides a way to unify fundamental forces. Some supersymmetric particles could even be the solution for dark matter.

Of course supersymmetry also predicts that there should be twice as many elementary particles than we actually observe. So why don’t we observe them? The answer lies in the fact that supersymmetric particles are more massive than regular particles, so at normal energies we simply don’t see them. But it turns out that in order to unify fundamental forces, the lightest of these supersymmetry particles should be observed in high energy collisions.

And therein lies the problem. The Large Hadron Collider has experimentally excluded the existence of supersymmetric particles at the expected energy levels. It is possible that supersymmetry particles exist at higher energies, but then supersymmetry can’t solve the hierarchy problem, which was the main reason for its introduction. It is also possible that supersymmetry is simply wrong. If supersymmetry is wrong, then string theory (and M-theory) are also wrong. So are the most straight-forward versions of loop quantum gravity.

So where do we go from here? Proponents of string theory have taken the view that supersymmetric particles are at energies higher than we expected. They may, in fact be at such high energies that any particle accelerators that could conceivably be built will not detect them. Of course that makes string theory effectively untestable. There are versions of LQG that don’t depend upon supersymmetry, but they also make predictions that are untestable. So it may be that neither approach will lead to clear scientific tests of their validity.

This is, of course, the big question regarding scientific discovery. Will there come a day when experimentally and observationally we can go no further? As humans we like to think that there is symmetry in the universe. That somehow our understanding of the cosmos can be unified into a single complete theory. But there’s nothing in the universe that requires such unification. Striving toward that goal has given us a deep understanding of physics, but we may face theoretical and experimental limits that prevent us from reaching the ultimate goal.

Even if that is the case, it won’t stop us from trying. Science is about pushing the limits of our understanding, and even in the face of seemingly insurmountable challenges, we can always keep pushing.

Miss the beginning of the series? It all starts here.