In the Red

If you toss a ball into the air, it will slow down as it rises. The Earth’s gravity pulls on the ball as it moves upward, causing it to slow down until it comes to a momentary stop at its highest point. Then it will begin to move downward, speeding up as it does. Suppose, then, that you were to shine a flashlight upward. What would happen? You might argue that gravity would pull on the photons, causing them to slow down, but we know that light has a constant speed, and can’t slow down. You might argue that since photons are massless gravity doesn’t affect them, but we know that the Earth’s mass, like any other mass, can cause light to change directions. So neither of these can be the answer. The real answer is pretty interesting, and it turns out to be one of the tests of Einstein’s theory of relativity.

To understand what happens to our beam of light, we need to look at gravity in a slightly different way. Normally we think of gravity as a force, but it can also be described in terms of energy. If you take a mass and drop it, it speeds up as it falls, thus gaining kinetic energy. When you toss a ball in the air, it slows down, thus losing kinetic energy. But energy is conserved, so energy gained or lost by the ball has to come from or go somewhere. This energy is typically called gravitational potential energy, since gravity has the potential to cause the ball to move. So rather than thinking of gravity as a force, we can see it as having a gravitational potential that can give or take away energy from the ball.

Hyperphysics

This brings us to the case of light. When we shine the flashlight upward, Newtonian gravity would say that the light is unaffected, since light is massless, but under general relativity light is affected by gravity, so as the light travels upward it must lose energy. But how is that possible if it can’t slow down? It turns out that the energy of light doesn’t depend upon its speed, but upon its wavelength. Red light with long wavelengths has less energy than blue light with short wavelengths. So as the light travels upward, its wavelength is stretched, and the light becomes more red. This is known as gravitational redshifting. For those of you wondering what this has to do with curved space, in general relativity the radial distance close to the Earth is shorter than the radial distance farther away. As the light moves upward its wavelength is stretched by the curvature of space due to gravity, which again means it is redshifted.

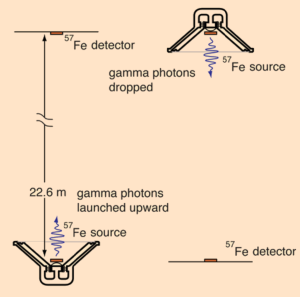
This effect is typically quite small, and it wasn’t confirmed until 1959, when Robert Pound and Glen A. Rebka performed an experiment with radioactive iron (Fe 57). This isotope emits gamma rays at a very specific wavelength. To detect these gamma rays they used a detector made of the same element. Since the detector can only catch the gamma rays at the same wavelength, any redshift of the gamma rays would make detection unlikely. Pound and Rebka showed that if you oscillate the detector at a particular frequency it would detect the emitted gamma rays. This is because the oscillation of the detector meant it saw the gamma rays redshifted due to relative motion. In this way they were able to determine how much the gamma rays were redshifted (or blueshifted) by its upward or downward motion. Their results agreed with Einstein’s predictions.

The Pound-Rebka experiment for gravitational redshift is now considered one of the three principal tests of general relativity. The other two are the precession of Mercury’s orbit and the deflection of light by gravity. As strange as general relativity may seem, it really is how the universe works.