In the Hole

Suppose you count down from five: 5, 4, 3, 2, 1, 0. Then what? You could just stop, or you could keep going -1, -2, -3 and so on. Mathematically there is nothing to prevent you from counting down below zero. Of course if you apply this idea to cupcakes, something changes when you reach zero. If you start with five cupcakes and start giving them away, you eventually run out. At that point you can’t give away any more. In this case you can’t count down past zero. Sure, you can hand out slips of paper with “I owe you a cupcake.” written on them, but it would be ridiculous to use the existence of negative numbers to claim that “negative cupcakes” exist and can be handed out to people.

A similar type of thing can occur in physical models. One example of this is the legendary “white hole” making the social media rounds of late. The basic idea of a white hole is that it is some kind of anti-black hole. Instead of capturing material and trapping it forever, a white hole spews material out. So they would constantly be generating material around it. There are even some speculations that black holes and white holes could be connected as a kind of wormhole.

All cool ideas, except for one problem. White holes don’t exist. I don’t mean they are hypothetical, but we don’t have evidence for them. I really mean they don’t exist. They are about as sensical as negative cupcakes.

The original idea of a white hole comes from the mathematics of general relativity. One of the key features of general relativity is that you can represent the structure of space and time in all sorts of different coordinate systems. This allows you to choose a coordinate system that makes your calculations easier, but it also means you have to be careful to recognize when you’re dealing with negative cupcakes.

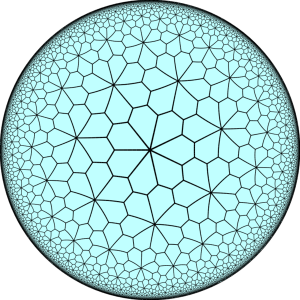Claudio Rocchini

When describing a simple black hole, one useful coordinate system is known as Kruskal–Szekeres coordinates. The coordinates are a good way to describe the spacetime around a simple black hole, but you can also extend them, just like you can count down to zero and keep going. Mathematically there is nothing to prevent you from extending the coordinates. When you do, you not only get a description of a black hole, you get a description of a white hole as a negative black hole. But that doesn’t make white holes real, or even hypothetical.

You can see a similar example in the figure here. It represents what is known as a hyperbolic coordinate system. It is a way to represent an infinite surface, and it does it by representing close areas as large, and more distant areas as tiny. Infinity is then represented as a finite area. But just because you can represent an infinite surface this way doesn’t mean you could walk off its edge.

Mathematics is a powerful tool in astrophysics, but you need to be aware of what it actually represents.