How to Build a Black Hole

Mark A. Garlick, University of Warwick

Yesterday we had a school project to build a star. Today let’s go for extra credit and see about building a black hole.

As you might recall, building a hypothetical star was basically a matter of gathering enough matter together so that it collapsed under its own weight. With enough mass (about 80 – 90 Jupiter masses) the interior pressure became great enough to start fusing hydrogen into helium, thus lighting our star. The fact that matter will undergo nuclear fusion given enough pressure actually makes building a black hole more difficult than building a star.

NASA, ESA, J. Hester and A. Loll

One way we could try to build our black hole is to simply create a very massive star and wait. As a star undergoes nuclear fusion, hydrogen is fused into helium. Over time the density of the star increases and the star burns hotter. Eventually the pressure is high enough that helium is fused into elements like carbon, nitrogen and oxygen. Those elements are eventually fused into heavier elements. But fusing elements beyond iron is an energy losing game, so there comes a point where a star can’t produce enough heat and energy to keep itself stable. For large stars, this means they undergo a supernova explosion. Such an explosion rips the star apart, but it can also compress the core of the star so that it collapses into a black hole.

That’s easy enough, but it doesn’t guarantee that a black hole will form. Our star might rip itself apart completely, or the core might not collapse into a black hole. To be sure we make a black hole, we’ll have to take a more gradual route. Instead of a really large star, let’s start with a star similar to our Sun.

Like larger stars, our Sun-like star will fuse hydrogen into helium for most of its lifetime. As it ages, it will gradually grow more dense and hot, and over time will start fusing helium into carbon, nitrogen and oxygen. After about 10 billion years it will run out of hydrogen and helium to fuse, and it will start collapsing under its own weight. For a short period of time it will try to fuse heavier elements, and as a result it will swell into a red giant star. But a Sun-like star simply doesn’t have enough mass to explode as a supernova, so in the end all it can do is collapse. But it doesn’t collapse into a black hole.

Because our old star doesn’t have a way to produce heat and energy through fusion, it once again relies upon hydrostatic pressure, where the pressure of the star’s material is balanced against its weight due to gravity. But instead of being a gas of hydrogen, it’s now a plasma, where the atoms have split into a mix of electrons and nuclei. The electrons move around much more easily than the nuclei, so as the star collapses it is the electron pressure that balances against gravity. When this happens our star becomes a white dwarf.

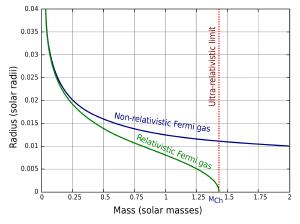
Wikipedia

To determine the size of our white dwarf, we just need to know how our plasma (technically known as a Fermi gas) behaves under temperature and pressure (its equation of state) which is quite well known. For a white dwarf about the mass of the Sun, it turns out to be about the size of Earth. It’s hard to imagine the entire mass of a star compressed into the volume of Earth, but we’ve observed lots of white dwarfs in our galaxy.

The pressure of electrons is extraordinarily strong, so in our simple model giving our white dwarf more and more mass will simply make it slightly smaller no matter how much mass we add. But in reality that’s not what happens. The more the Fermi gas of electrons is squeezed, the faster the electrons move. A white dwarf is so dense, and the electrons are moving so quickly that they approach the speed of light. This means we have to take relativity into account.

One of the important consequences of relativity is that mass and energy are related. As a result, gravity acts not just on the mass of an object, but also its energy. Usually the energy contribution is negligible, but when the electrons approach the speed of light their energy becomes much larger than their mass. The faster the electrons move, the heavier they get. So the very act of speeding up to create more pressure against gravity actually ends up helping gravity. There comes a point where the gravitational weight gained is more than the pressure the electrons can make, and the Fermi gas completely collapses. The point at which this occurs is about 1.44 solar masses, which is known as the Chandrasekhar limit. So we simply add mass to our white dwarf beyond that limit, and our white dwarf will collapse. But it still won’t collapse into a black hole.

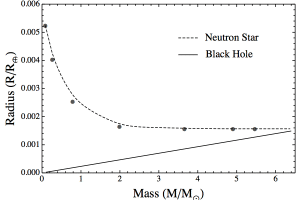
BK

In a white dwarf, the main pressure is caused by the electrons of the plasma, while the nuclei play a much smaller role. But when a white dwarf collapses the pressure of the nuclei is still there. The electrons collapse and merge with protons to create neutrons, and what remains is basically a Fermi gas of neutrons. The resulting neutron star is again a balance of pressure and weight, only this time it is neutron pressure vs gravity. The equation of state for neutrons is similar to that of electrons, so we can again determine the size of our neutron star given a particular mass. What we find is that a star of about 2 solar masses would have a diameter of about 15 kilometers, which is roughly the size of a small city like Rochester NY. Because neutrons are much heavier than electrons, we’d have to add much more mass to our star to approach the point where the neutrons collapse. But it turns out a black hole forms well before that point.

In a simple neutron gas model, the size of a neutron star would level off at about 10 – 15 kilometers even as we add more and more mass. But as we add mass, the density of the star increases to the point where a black hole must form. Technically, a black hole will form if your mass is within a sphere of a particular radius known as the Schwarzschild radius. For any given mass you can calculate this radius quite easily. The Schwarzschild radius of the Earth, for example, is about about a centimeter, so an Earth-mass black hole would be about the size of a large marble.

To create a black hole, we simply need to add mass to our neutron star until its Schwarzschild radius is larger than the radius of the neutron star. This limit is known as the Tolman-Oppenheimer-Volkoff (TOV) limit. In very simple models this limit is about 6 solar masses, but more realistic models put the limit at about 3 solar masses. We’ve observed a lot of neutron stars in the galaxy, and 3 solar masses appears to be about the limit.

So creating a black hole is much like creating a star. It’s a matter of getting enough matter into a small enough volume. That’s how nature does it, and it’s worked out pretty well so far.