How Does Gravity
Escape a Black Hole?

Paramount Pictures

Here’s the deal: nothing can travel faster than light. A black hole traps everything including light. So how does gravity escape a black hole? It’s a great question, and a perfectly reasonable one given most people’s understanding of gravity. The answer is that gravity doesn’t work the way you probably think it does.

The most common way to think of gravity is as a force between two masses. For example, the Earth exerts a gravitational force on the Moon, and the Moon pulls back on the Earth in return. This “force model” of gravity is what Newton used to develop his law of universal gravity, which stood as the definite theory of gravity until the early 1900s and is still used to this day. But built into this model of gravity are some assumptions that we can explore by playing the “what if?” game.

Suppose we had a universe with a single mass. Imagine empty space extending as far as you like, with a single mass in the center (which we’ll call Bob). Would such a mass have gravity? If gravity is a force of one object on another object, then the answer would be no. There’s no other mass for Bob to pull on, so there’s no gravitational force. If we add another mass to our universe (call this one Alice), then Bob and Alice would each exert a force on each other, and gravity would exist. But gravity would only exist between Bob and Alice, and nowhere else in our empty universe.

Hyperphysics

One of the problems with this force model is that it requires masses to exert forces on other masses across empty space. This “action at a distance” problem was resolved in part by Pierre-Simon Laplace in the early 1800s. His idea was that a mass must reach out to other masses with some kind of energy, which he called a field. Other masses would sense this field as a force acting upon them. So if we again imagine our Bob mass in a lonely universe, we would say that Bob has a gravitational field surrounding it, even if there were no other masses in the universe. This eliminates the need for action-at-a-distance, because when we put our Alice mass into the universe, it simply detects whatever gravitational field is at its location, and experiences a force. We know the gravitational field is due to Bob some distance away, but Alice simply knows there is a gravitational field at its location.

Both the force model and field model of Newtonian gravity give the same predictions, so experimentally there’s no real way to distinguish one from the other. However fields are often an easier concept to work with mathematically, and fields are also used to describe things like electricity and magnetism, so we generally think of Newtonian gravity as a field.

Wikipedia

But this raises another question. Suppose in our Bob and Alice universe we suddenly shift Bob’s position. How long will it take for Alice to recognize the change? In other words, if we change the position of Bob, at what speed does the change propagate through the gravitational field? When Laplace looked at this idea he found that changes in a gravitational field had to happen instantly. The “speed of gravity” would have to be infinite. For example, if gravity traveled at the speed of light, the Earth would try to orbit the point where the Sun was 8.3 minutes ago (the time it takes light to travel from the Sun to Earth). As a result, Earth’s orbit would become unstable over time.

At the time, the idea of gravity acting at infinite speed wasn’t seen as a problem. In fact, it was used as an argument against alternative gravity ideas proposed at the time. But in the early 1900s, Einstein developed his special theory of relativity, which (among other things) required that nothing could travel faster than light. If that’s the case, then there’s something wrong with our theory of gravity. By 1915 Einstein had developed a new model of gravity known as general relativity, which satisfied both Newton’s gravitational model and special relativity.

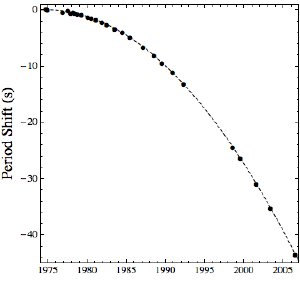
Brian Koberlein

According to theory, for example, when two large masses such as neutron stars orbit each other, they should produce gravitational waves that radiate away from them. These gravitational waves should travel at the speed of light. There have been experimental attempts to detect such gravitational waves, but they have been unsuccessful so far. We have, however, found indirect evidence of gravitational waves. By observing a binary pulsar, we have observed its orbit decay slightly over time. This orbital decay is due to the fact that gravitational waves carry energy away from the system. The rate of this decay matches the prediction of general relativity perfectly. Since this rate of decay depends crucially on the speed of gravitational waves, this is also indirect confirmation that gravitational waves move at the speed of light.

But if gravity moves at the speed of light, doesn’t that mean that planetary orbits should be unstable? Actually, no. When Laplace studied finite-speed gravity, he considered only the effect of the speed of gravity, which is what leads to his result, but in special and general relativity, the finite speed of light leads to other effects, such as time dilation due to relative motion, and the apparent change of mass due to relative motion. Mathematically these effects arise because of a property known as Poincaré invariance. Because of this invariance, the time delay of gravity and the velocity-dependent effects of time and mass cancel out, so that effectively masses are attracted to where a mass is. This canceling effect means that for orbital motion it is as if gravity acts instantly.

But wait a minute, how can a gravitational field have a finite speed and act instantly at the same time? A gravitational field can’t, but in general relativity, gravity is not an energy field.

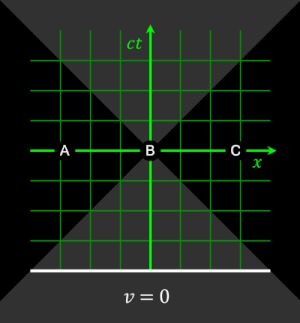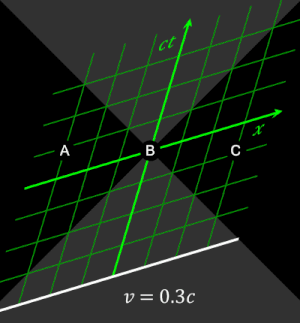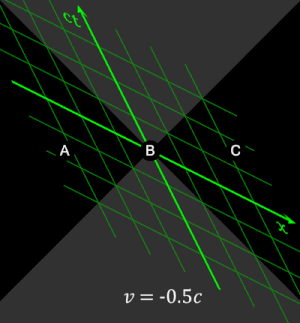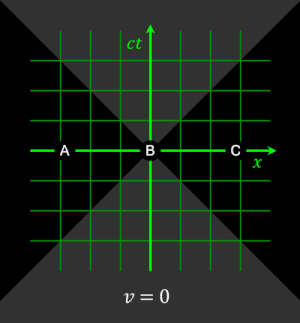
Wikipedia

Since long before Newton, it was generally assumed that objects and energy fields interacted in space at particular times. In this way, space and time can be seen as a background against which things happen. Space and time were seen as a cosmic grid against which anything could be measured. In developing special relativity, Einstein found that space and time couldn’t be an absolute background. In Newton’s view, two events seen to occur at the same time will be seen to be simultaneous for all observers. But Einstein found that the constancy of light required this concept of “now” to be relative. Different observers moving at different speeds will disagree on the order of events. Rather than a fixed background, space and time is a relation between events that depends upon where and when the observer is.

Christopher Vitale

This principle carried forward into Einstein’s theory of gravity. In general relativity, gravity is not an energy field. Instead, mass distorts the relations between space and time. If we go back to our earlier example, if we place mass Bob in an empty universe, the relations of space and time around it are distorted. When we place mass Alice nearby, the distortion of spacetime around it means that moves toward mass Bob. It looks as if Alice is being pulled toward Bob by a force, but it’s actually due to the fact that spacetime is distorted.

As physicist John Wheeler once said, “Spacetime tells matter how to move; matter tells spacetime how to curve.”

This is how gravity can seem to act instantly while gravitational waves seem to travel at the speed of light. Gravity isn’t something that travels through space and time. Gravity is space and time.

A black hole is an extreme distortion of space and time due to a very dense mass. Such a spacetime distortion can prevent light and matter from ever escaping. But the spacetime distortion is also gravity. It doesn’t need to escape the black hole, because it is the black hole.

That’s the thing about science. Sometimes a simple question will pull you toward an unexpected answer.