Highland Fling

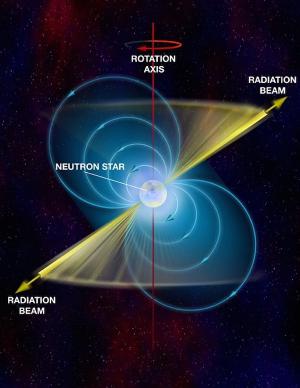
NASA/Goddard Space Flight Center

Earlier I talked about millisecond pulsars, and the way in which they might gain such rapid rotation. Another property of millisecond pulsars is that they demonstrate very clearly that pulsars are neutron stars. It all has to do with their rapid rotation and the physics of centripetal (or centrifugal) force.

When you stand on the Earth, there are two basic forces acting on you. The first is gravity, where the attraction of Earth’s mass tries to pull you to the center of our planet. The second is the ground, which prevents you from moving through it by pushing up on you. This is often called the normal force. Standing on the ground, these two forces are in balance. The weight of gravity is countered by the normal force of the ground, which is why you can stay put.

If the Earth weren’t rotating, then these two forces would be equal in magnitude. But since the Earth rotates, the normal force is very slightly smaller than the attraction of gravity. Just how much smaller depends on where you are on the Earth, but it is smallest if you are standing on the equator. You can see why that is if you’ve ever been in a car going around a corner. As the car turns, it feels like you are being pulled slightly outward, away from the turning car. This is sometimes called a centrifugal force, and it has to do with the fact that your body (like any object with mass) would like to keep moving in a straight line at a constant speed. To change your direction (and keep you in your seat) the car has to push you in the direction of the turn. Whenever you are pushed in some direction, it feels like you are being pulled in the opposite direction, so it feels like you are being pulled outward. A similar thing occurs when your car accelerates, and it feels like you are being pulled back into your seat.

As you stand upon our rotating planet, a similar thing occurs. You are moving around in a circle, once per day, so your direction is always changing. Your body would like to keep moving in a straight line, but Earth’s gravity keeps changing your direction. Earth’s gravity is more than strong enough to overcome your centrifugal force, so the normal force of the ground also acts to keep you on the ground. But the normal force doesn’t have to counteract all of gravity, just the extra gravity beyond the centrifugal force.

NRAO

Now suppose we could spin our spherical world faster and faster. As we are standing on its surface, we would have a tendency to fly off the world due to its rotation. The gravity is stronger than the centrifugal force, so we stay put. But if we could spin the world faster and faster, we would reach a point where the centrifugal force is equal to the force of gravity. Spin the world any faster, and we would fly off. Earth’s gravity wouldn’t be strong enough to hold us. The surface gravity of a planet or star depends upon its density, so far a given density for a planet/star, there is a maximum rate of rotation. Any faster and it would fly apart. Put another way, if we measure the rotation of a planet or star, we know its minimum density.

When we do the math, we find we can calculate that minimum density in grams per cubic centimeter by taking 140 million and dividing it by the square of an object’s period in seconds. So for the Earth, the period is 24 hours or 86,400 seconds. Plug that into our equation and we get a minimum density of about 0.02 g/cc. The Earth’s real density is about 5 g/cc, well above that minimum.

Pulsars are kind of like cosmic light houses. As they rotate they sweep out a beam of radio waves from their magnetic poles. If those poles are pointing in our direction, we can hear each rotation as a pulse. The fastest millisecond pulsar has a rotation of 716 times a second, or a rotational period of 1.4 milliseconds. Plug that into our equation, and you get a minimum density of about 7 x 10¹³ g/cc. Thats that’s about 7 billion kilograms per sugar cube volume, which is an unimaginably high density. It also happens to be a bit less than the density of atomic nuclei.

So pulsars are as dense as atomic nuclei, only several kilometers in diameter. We call them neutron stars.