Gravity Check

Newton’s law of gravity states that between any two masses there is a gravitational force. The strength of that force depends not only on the masses, but on the distance between those masses, following what is known as an inverse square relation. That is, if you double the distance between two masses, their gravitational attraction will be a quarter of what it was. If you halve the distance between two masses, their attraction will be four times stronger. Newton felt that this inverse square relation was exact, but is it?

One of the ways we know Newton’s gravity works is through the motion of the planets. Masses like the planets and Sun are attracted to each other by gravity’s inverse square relation, and thus their motion follows a relation known as Kepler’s laws. We have seen that this holds not only for the planets and moons in our solar system, but also for other stars orbiting each other, exoplanets orbiting their star, and even stars orbiting the supermassive black hole in the center of our galaxy. So Newtonian gravity works very, very well.

For large masses we know that the inverse square relation for gravity isn’t quite exact. For example, Mercury and the Sun are massive enough and close enough that Mercury’s orbit deviates slightly from a simple elliptical orbit. This deviation was the first evidence of general relativity. We also know that the orbit of massive neutron star orbiting with another star will decay in a way that violates Newtonian gravity (but agrees with general relativity). Newtonian gravity works very well, but for massive objects general relativity is more accurate.

What about for small masses on very short scales?

We know that on very small scales Newtonian physics is inaccurate, and we need to use quantum mechanics. One common feature of quantum mechanics is that rather than being smooth and continuous, objects can be constrained into discrete (quantum) states. We see this, for example, in the light emitted by an atom. Rather than being a continuous range of wavelengths, the emitted light can only be at particular wavelengths. This is due to the fact that an electron in an atom can only have particular energy levels. When an electron drops from a higher energy level to a lower one, it releases a photon of a particular wavelength.

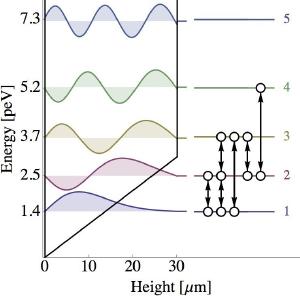
T. Jenke et al

On very small scales, gravity is also be quantized. We don’t have a complete theory of quantum gravity, but for weak gravitational fields such as Earth’s, it can behave similar to the quantum energy levels of an electron in an atom. In a new paper in Physical Review Letters, this fact was used to measure Newton’s inverse-square gravity to the highest precision yet.¹

What the team did was to create a “gravitational atom” by bouncing between two mirrors (not mirrors in the way we usually think, but rather a surface that can reflect neutrons). These particular neutrons were ultra-cold, so their bounces were very small and were very low energy. Because of this the energy of these neutrons were quantized. Basically, instead of being able to bounce to any height like a rubber ball, they could only bounce to specific (quantum) heights. In other words, the gravitational energy of the neutrons were quantized in much the same way that the energy of electrons are quantized in an atom.

The team was then able to measure these energy levels very precisely, using a method known as resonance spectroscopy. Since the energy levels of the neutrons depend on gravity, any deviation of gravity from Newton’s inverse square relation would show up as a shift in the energy levels. What the team found was that the energy levels matched Newtonian gravity to the limits of their measurements.

What’s interesting about this result is that it puts constraints on certain forms of dark energy and dark matter. For example, one model of dark energy, known as quintessence, proposes that dark energy is a scalar energy field. One prediction of quintessence is that it would cause gravity to deviate from an inverse square relation at small energy levels. This experiment rules out quintessence unless its interaction is very weak. One idea for dark matter is a particle known as an axion. This type of particle would also interact at low energy levels, causing a deviation from Newton’s gravity. This experiment rules out axions unless their interaction is extremely weak.

So it turns out that on very small scales Newtonian gravity still works, and that means that dark energy is not likely to be due to quintessence, and dark matter is not likely made of axions.