Frozen Star

NASA / S. Charbinet

Last time I talked about how black holes can exceed a maximum luminosity known as the Eddington limit. The Eddington limit is the point where a star is so bright that its light pressure balances out the gravitational pressure of the star. Today I’ll talk about another limit known as the Chandrasekhar limit. This one puts a limit on how massive a star can be when it dies, and it relies on a bit of quantum mechanics.

When a typical star is in its active lifetime (main sequence), the gravitational weight of its mass is balanced by the heat and pressure generated by fusion in its core. This is a stable period for a star, and can last for billions of years (or in the case of red dwarfs, trillions). But eventually a star runs out of hydrogen to fuse, and it can’t sustain the heat and pressure in its core. With no more fusing core, the old star is basically just a hydrostatic mass. The key difference is that the density is so high it isn’t a regular ball of gas, but rather a gas of plasma. All the ions and free electrons act somewhat like a regular gas, but with one big exception: the electrons and ions obey the Pauli exclusion principle.

In broad terms the Pauli exclusion principle means that the electrons can’t occupy the same state. It is kind of like musical chairs where everyone jostles each other to find a seat, and two people can’t share the same seat. The exclusion principle also applies to the ions, but it turns out that the electrons need bigger chairs, so it’s the electrons we most have to worry about. As a result of the exclusion principle the electrons exert a degeneracy pressure to keep all the other electrons out of their chair. You can therefore treat the electrons as a simple gas with a pressure due to the exclusion principle. Such a star is sometimes called a degenerate star, but it is more commonly known as a white dwarf.

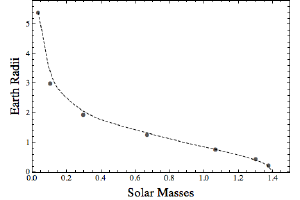BK

So to model such a star, we just need gravity and the equation of state (a description of the pressure) for our electron gas. What we find is that the more mass a white dwarf has, the smaller its radius. This is exactly what we would expect, since more mass means stronger gravity, which means all those degenerate electrons are squeezed harder. But when the mass reaches about 1.4 solar masses, the electrons are squeezed so tightly that the resulting radius is zero. At this limit the electron pressure can’t withstand gravity. This limit is known as the Chandrasekhar limit (named after its discoverer). Above this limit and the electrons are squeezed into the protons in the ions, leaving a massive ball of neutrons known as a neutron star. Actually, it isn’t quite that simple, but you get the idea.

Since a white dwarf can’t produce heat through fusion or anything else, once it forms it gradually cools. Since white dwarfs are small they don’t have a lot of surface area, so they cool rather slowly, but given enough time such a star would cool to the background temperature of the universe, becoming a cold and dark frozen star.