Far from the
Madding Crowd

Gabriela Secara, Perimeter Institute CC-BY-4.0

Last time I wrote about new data that overturns the standard cosmological model. Before anyone starts dusting off their fringe cosmological models, we should note what this new study doesn’t overturn. It doesn’t say the Big Bang model is wrong, nor does it say that the Universe isn’t expanding or that Hubble’s redshift-distance relation needs to be thrown out. It really only says that our Hubble constant model is wrong.¹ But we already knew that thanks to a little thing known as the Hubble tension. These new results could solve that mystery as well.

Before we dive into the Hubble tension, let’s talk about the Hubble constant and the Friedmann–Lemaître–Robertson–Walker (FLRW) metric. In 1929, thanks to the work of Henrietta Leavitt and others, Edwin Hubble was able to show that—beyond the local group—the more distant a galaxy is the greater its redshift. He found the relation between distance and redshift was linear, leading him to propose a cosmological constant, now known as the Hubble constant.²

In 1917 Einstein had added a cosmological constant to general relativity to balance out the gravity of galaxies. Like most astronomers at the time, Einstein assumed the Universe was in a steady state. Without the constant, a steady state wasn’t possible. With Hubble’s discovery, Einstein tossed the idea, but Alexander Friedmann and Georges Lemaître discovered independently that solutions to the Einstein’s equations with a cosmological constant could describe an expanding universe that begins with a Big Bang. In 1935, Howard Robertson and Arthur Walker proved that the FLRW metric is the only solution to GR that describes a uniform expanding universe.³ This is the metric used in the standard model. Since the FLRW metric uses Λ as the symbol for the cosmological constant, it’s the ΛCDM model.

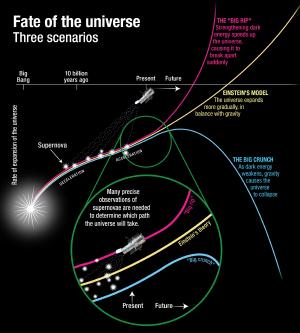NASA and A. Feild (STScI)

The Hubble constant H₀ and the cosmological constant Λ are related, but they aren’t exactly the same. The rate of cosmic expansion depends on several things: the cosmological constant (dark energy), the amount of dark matter and regular matter in the cosmos, and the distribution of that matter. In simple terms, matter tries to pull everything together, while dark energy tries to push everything apart, and the balance between the two gives the rate of cosmic expansion, or Hubble constant. Naturally, since the early Universe was denser than the current Universe, you’d expect the rate of cosmic expansion to increase a bit over time. This is why the discovery of an accelerating cosmic expansion was such a big deal. It proved the existence of dark energy and the cosmological constant.⁴ This is also why the Hubble constant is often called the Hubble parameter these days.

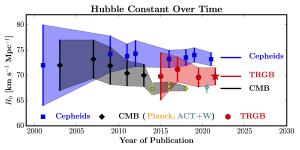Wendy Freedman

For decades observational evidence supported the ΛCDM model. But in the past decade or so our measurements of the Hubble parameter became problematic. There are several ways to find the Hubble parameter, but the big three are distant supernovae, the cosmic microwave background (CMB), and a pattern in clustering galaxies known as Baryon Accoustic Oscillation (BAO). The supernovae observations give us an expansion rate of about H₀ = 71 – 75 (km/s)/Mpc, while the scale of fluctuations in the CMB give a value of H₀ = 67 – 68 (km/s)/Mpc. The BAO measure gives a result of H₀ = 66 – 69 (km/s)/Mpc. This is what we call the Hubble tension. These results should agree, but they absolutely don’t.

Now you might think this means the supernova measurements are wrong, but things aren’t so clear. All three of these methods rely upon assumptions about models and evidence hierarchies. Early on, astronomers figured better data would bring the values together, but they only got worse. Even other methods using things such as gravitational lensing or astronomical masers contradict each other. Which is why this new study is so interesting.

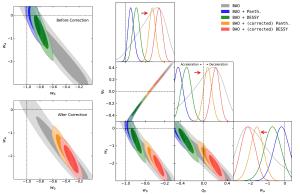Son, et al

The work doesn’t make a full survey of how their results would change various Hubble measurements, but it does look at the big three. When the age of host galaxies is taken into account, the supernova measure shifts much closer to the other two. The team even did an initial test of their results using host galaxies of about the same age regardless of their redshift, and the results are slightly better. Accounting for galactic age in supernova data appears to solve much of the Hubble tension.

The authors point out that their results are still somewhat tentative. There are only about 300 distant galaxies that have both an observed supernova and a spectrum from which you can determine the age of the host galaxy. That’s a small sample size, so while the results are compelling, they aren’t conclusive. The good news is that when Rubin Observatory comes online later this year we’ll be able to determine the ages of thousands of distant galaxies. Within a few years we’ll know whether this new model holds up. If it does, then we’ll have to toss the cosmological constant as the single source of dark energy.

So what then? If ΛCDM is wrong, what alternative is there? I’ll talk about that next time.