Could We Ever Build
a Time Machine?

CERN

In fiction there are lots of ways to travel through time, from reaching 88 miles per hour in a DeLorean to walking through a circle of ancient Scottish stones. While the idea of time travel is centuries old, it had no basis in reality. But when Einstein developed his gravitational theory of general relativity, some physicists began to wonder if time travel might actually be possible.

One of the central ideas of general relativity is that there is no cosmic clock. While we always experience time at a normal rate, our rate can seem faster or slower relative to another observer. The relations between space and time are distorted by the presence of mass, and for objects such as black holes that distortion can be extreme. So could time be warped in such a way that it loops back on itself? In the 1970s, some physicists began to study this question in a serious way. Not as a serious effort to build a time machine, but as a way to explore the broader aspects of relativity.

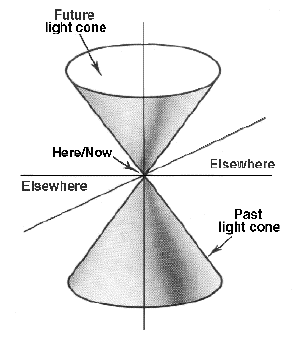
Matt Visser

One of the ways we can study the behavior of space and time is through what are known as light cones. Imagine a flash of light at a single point. The light would travel away from that point in all directions, so that the flash of light is an expanding sphere. Since nothing can travel faster than the speed of light, then that expanding sphere marks the limit of your influence. In general, you can’t move outside that sphere, because you can’t travel faster than light. Since it’s difficult to visualize 4-dimensional spacetime, we often imagine space as a two-dimensional surface, like a sheet of paper, and time as being the third dimension. You can imagine it as a stack of paper, with a cartoon drawing on each page, then flipping through the drawings would make them appear to move. Each sheet of paper would be a moment in time, and different pages in the stack of paper would be different moments in time. The only difference is that time is a continuum rather than discrete instants. In this visualization, an expanding sphere of light would start at a point, and with each higher page would be a larger and larger circle. If you flipped through the pages you would see an expanding circle of light. If instead you could see through the paper and just look at the circles, then you would see they form a cone starting at a particular point. This is known as a light cone, and it defines the limit of influence of an object at the point. An object at the starting point cannot influence anything outside of that light cone, nor can it ever move beyond the limit of that light cone.

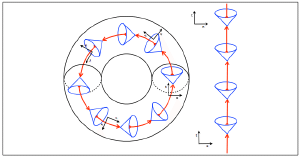
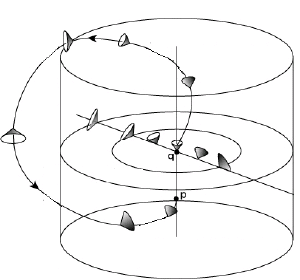
Ben Tippett and David Tsang

The path of an object that stays within the light cone is called “timelike,” since it follows the motion of the object through time. Relativity requires that the path of all objects be timelike. So in general relativity the question becomes whether light cones can be warped in such a way that the timelike path of an object connects with its own past. If you found yourself in such a wibbly-wobbly spacetime it would be possible to meet your younger self. Such a loop is known as a closed timelike curve (CTC), and would be an actual time machine.

Matt Visser

Interestingly, CTCs are absolutely possible within the theory of general relativity. One place where CTCs appear is in a solution to Einstein’s gravity equations known as the Gödel universe. This is a general relativistic description of a universe with an inherent rotation to it. Of course we know observationally that our universe doesn’t have such an inherent rotation, so the Gödel model doesn’t match reality. CTCs also appear inside a rotating black hole. A rotating mass causes space and time to swirl around it a bit (an effect known as frame dragging). Once you are within the event horizon of the black hole this swirling becomes strong enough there are CTCs. But this is only true if there is a singularity within the black hole, and its most likely that quantum physics prevents such a singularity from forming.

Discovery

It doesn’t look like time machines occur naturally, so what about creating an artificial one? In the 1980s, Kip Thorne proposed using a wormhole as a time machine. Wormholes are purely hypothetical, and if they did exist they would collapse before you could travel through one. But Thorne found that if you could magically prevent a wormhole from collapsing, it could be used to create a time machine. Thorne’s model was simply a “what-if” scenario intended to test the limits of general relativity, but others such as Ron Mallett think it might be possible.¹ Mallet has found a solution to general relativity that allows for CTCs without an event horizon. What Mallett has shown is that light can curve space and time in the same way as mass. By creating a rotating ring of laser light it is possible to distort space and time in a way similar to the way it is distorted by the rotating mass of a black hole, but without the black hole. This, he argues, opens the door to the possibility of creating a time loop. Critics have pointed out that Mallet’s solution still contains a singularity, so it isn’t a valid physical solution, but Mallett argues the singularity in his solution is an artifact that doesn’t affect the physics.

As for who’s right, time will tell. It’s easy to create a theoretical time machine within general relativity, the physics of matter and energy seem to prevent the creation of a real time machine. So could we ever build a time machine? Almost certainly not.

But that’s not a no.