The Brilliance
of Scientific Assumptions

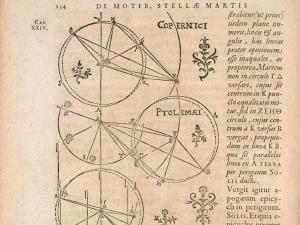
Johannes Kepler

In the early 1600s, Johannes Kepler proposed a new set of rules to describe the motions of the planets. Rather than using epicycles and offset circles, Kepler proposed that planets moved in ellipses around the Sun. As the story is usually told, the model that came to be known as Kepler’s laws of planetary motion revolutionized astronomy. But that isn’t the case. At the time, only the orbits of Mercury and Mars were known to be non-circular, and some astronomers noted that oval orbits worked just as well as elliptical ones.

The view of Kepler’s model wasn’t solidified until after Isaac Newton developed his theory of mechanics of moving bodies. Using his laws of motion and universal law of gravitation, Newton was able to derive Kepler’s laws as a good description of planetary motion, and also as a consequence of a more fundamental, underlying mechanism. For a single perfectly spherical planet orbiting a perfectly spherical Sun, Kepler’s laws describe the motion of the planet exactly. Of course, the Sun and planets aren’t perfectly circular, and they interact gravitationally with one another, so planetary motion doesn’t match Kepler’s laws exactly. This raises an interesting point about how physical models are developed.

The Wonders Series (BBC)

In his universal law of gravitation, Newton proposed that any two masses are gravitationally attracted to each other, and that the strength of their attraction depended on the inverse of their distance to the power of 2. Not 1.99, not 2.01, but exactly 2. Given the limits of observation at the time, small deviations from 2 worked just as well. In fact Newton showed that the motion of the Moon around the Earth could be described as a gravitational attraction to the power of 2.016. He then went on to show that this deviation from 2 could be accounted for by the gravitational attraction of the Sun. Newton was able to show that the attraction of gravity had to be close to an inverse square relation, so he assumed the relation was exact.

As our understanding of Newtonian motion improved, and our measurements of planetary motion became more precise, we could begin to observe the gravitational effects between planets. Sixty years after Uranus was discovered in 1781, John Couch Adams and Urbain Le Verrier calculated the gravitational effects of a more distant body on the planet’s motion. This led to the discovery of Neptune.

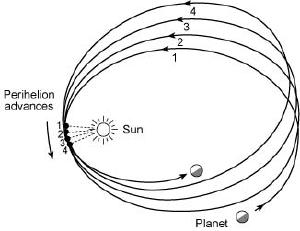
Michael Richmond

But there were some phenomena Newtonian gravity couldn’t address. Observations of the planet Mercury shows that its orbit shifts (precesses) by about 574 arcseconds per century. Much of this shift could be accounted for by gravitational interactions from other planets and the fact that the Sun is not perfectly spherical, but there was still about 43 arcseconds that couldn’t be accounted for. One idea was that there must be a planet even closer to the Sun than Mercury. In the late 1800s several astronomers looked for such a planet, which was tentatively given the name Vulcan.

Kenneth R. Lang

An alternative solution is that Newton’s inverse-square assumption was wrong. Astronomer Simon Newcomb, for example, demonstrated that Mercury’s anomalous precession could be accounted for by “correcting” Newton’s equation to be to the power of 2.0000001574. Most astronomers at the time thought such an idea was unlikely, and later observations of lunar motion showed that Newcomb’s correction didn’t work for the Moon. So a planet Vulcan seemed to be the likely solution. But it turns out that Newcomb was closer to the truth. When Einstein developed the theory of general relativity, one of the predictions was that Newton’s inverse-square relation wasn’t exact. From this, Einstein was able to show that the Mercury anomaly was due to relativistic corrections.

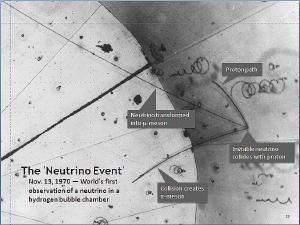
A similar thing can be seen in the history of neutrinos. In the late 1800s Marie Curie and others began to study radioactive decay. They found that certain elements were radioactive, and could transform from one element to another while emitting high-energy rays. While the mechanism wasn’t understood, it seemed to do with the equivalence between mass and energy, which Einstein famously summarized in the equation E = mc2. But this raised more questions than it solved.

Argonne National Laboratory

For example, caesium radioactively decays into barium, and in doing so emits a high-energy electron (beta ray). The mass of a caesium atom is greater than that of barium, so the “lost mass” must somehow be converted to energy. But energy was assumed to be conserved. If that’s the case, then the emitted electron should have the same energy every time. But experiments demonstrated that the electron could have a wide range of energies, so it looked like conservation of energy was wrong.

Some physicists, such as Niels Bohr, thought that the assumption about conservation of energy could be wrong. Rather than holding true exactly, energy might only be conserved on average, and variations in the electron energies were due to some quantum fluctuation. However Wolfgang Pauli proposed the existence of an additional particle. Thus beta decay must emit both an electron and a small uncharged particle we now call the neutrino. Being uncharged, it was effectively invisible at the time.

Inventing particles to make your assumption work might seem like a bad idea, but it turns out to be correct. By 1956 neutrinos were detected in a nuclear reactor, and in more recent decades we’ve begun to develop neutrino astronomy.

As our understanding of quantum mechanics and particle physics grew, another assumption about neutrinos was put to the test. By the 1970s we had developed a theory of fundamental particles known as the Standard Model. This model unified our understanding of electromagnetism and the nuclear forces known as the strong and weak. It described all known elementary particles, and even predicted new particles that were eventually observed. According to this model, the mass of a neutrino was exactly zero. There were variations of the model where neutrinos have mass, but all experiments seemed to show a massless neutrino. If neutrinos did have mass, it would need to be very, very close to zero to agree with experiments, and that seemed unlikely.

Kamioka Observatory

As neutrino detectors became more precise, it became clear there was a problem with the model. When we observed the level of neutrinos coming from the Sun, we found it was about a third the expected level. This result was repeatedly confirmed, and it became known as the solar neutrino problem. One solution to this problem was to drop the assumption that neutrinos were massless. Even the tiniest amount of mass would mean neutrinos could not move at the speed of light, and could therefore change from one species (electron, muon or tau) into another over time. This effect is known as neutrino oscillation. It wasn’t until 1998 that neutrino oscillation was confirmed, but with that discovery the solar neutrino problem was resolved.

It might seem counterintuitive for scientists to rely upon assumptions, but they are central to the progress of science. Observational and experimental evidence can never confirm an exact value, but can only validate and put constraints on any possible deviations. So in addition to the strict observational and experimental evidence, we are guided by mathematical elegance, or utilitarian simplicity. Assuming a relation to be exact can move us forward.

So can discovering our assumptions are wrong, which is part of the reason why we keep testing them. Has the speed of light always been constant? Observations of distant gas clouds show that it has been constant to within 1 part in 10 billion over the last 7 billion years. If light isn’t constant, then our understanding of the early universe will be rewritten. Is the universe flat? Observations of the cosmic microwave background show that it is to within 4 parts in 1000. If we find the universe deviates from flatness, then it could be evidence of other universes or that our own universe is finite in extent. Is charge conserved? Neutron decay shows that it is to within 8 parts in 1 octillion. If we find charge isn’t conserved it could open up an entirely new world of particle physics.

That’s what makes scientific study so powerful. We make assumptions based upon the evidence we have, and develop theories to describe the universe around us. But we also keep testing our assumptions. We keep working to develop better theories. We always, always keep in mind that our assumptions might just be wrong.

And when we find they are—even if it’s just a single piece of evidence that points the way—whole new fields of research can open up.