Black Holes Tell No Tales.
Or Do They?

ZME Science

You’ve just committed the perfect crime. No one saw you do the crime, and you left no trace. The perfect crime. The only way anyone could prove you did it is by finding the journal of your master plan. Get rid of the journal, and you are scot free. You want to be absolutely, 100% certain that the information it contains is permanently destroyed. Suppose you toss your journal into a black hole. Would that destroy all traces of your plan?

Fox Television

The answer to this hypothetical scenario lies at the heart of the information paradox. Stated more generally, the paradox raises the question: can information be destroyed? The question is important because it strikes at the very heart of what science is. Through science we develop theories about how the universe works. These theories describe certain aspects of the universe. In other words they contain information about the universe. Our theories are not perfect, but as we learn more about the universe, we develop better theories, which contain more and more accurate information about the universe. Presumably the universe is driven by a set of ultimate physical laws, and if we can figure out what those are, then we could in principle know everything there is to know about the universe. If this is true, then anything that happens in the universe contains a particular amount of information. For example, the motion of the Earth around the Sun depends on their masses, the distance between them, their gravitational attraction, and so on. All of that information tells us what the Earth and Sun are doing.

In the last century, it’s become clear that information is at the heart of reality. For example, the second law of thermodynamics. In its simplest form it can be summarized as “heat flows from hot objects to cold objects”. But the law is more useful when it is expressed in terms of entropy. In this way it is stated as “the entropy of a system can never decrease.” Many people interpret entropy as the level of disorder in a system, or the unusable part of a system. But entropy is really about the level of information you need to describe a system. An ordered system (say, marbles evenly spaced in a grid) is easy to describe because the objects have simple relations to each other. On the other hand, a disordered system (marbles randomly scattered) take more information to describe, because there isn’t a simple pattern to them. So when the second law says that entropy can never decrease, it is saying that the physical information of a system cannot decrease. What began as a theory of heat has become a theory about information.

Is Information Conserved?

Wikipedia

It’s generally thought that information can’t be destroyed because of some basic physical principles. The first is a principle known as determinism. If you throw a baseball in a particular direction at a particular speed, you can figure out where it’s going to land. Just determine the initial speed and direction of the ball, then use the laws of physics to predict what its motion will be. The ball doesn’t have any choice in the matter. Once it leaves your hand it will land in a particular spot. Its motion is determined by the physical laws of the universe. Everything in the universe is driven by these physical laws, so if we have an accurate description of what is happening right now, we can always predict what will happen later. The future is determined by the present.

The second principle is known as reversibility. Given the speed and direction of the ball as it hits the ground, we can use physics to trace its motion backwards to know where it came from. By observing the ball now, we can know from where the ball was thrown. The same applies for everything in the universe. By observing the universe today we can know what happened billions of years ago. The present is predicated by the past.

These two principles are just a precise way of saying the universe is predictable, but it also means information must be conserved. If the state of the present universe is determined by the past, then the past must have contained all the information of the present universe. Likewise, if the future is determined by the present, then the present must contain all the information of the future universe. If the universe is predictable, then information must be conserved.

yellowtang.org

Now you might be wondering about quantum mechanics. All that weird physics about atoms and such. Isn’t the point of quantum mechanics that things aren’t predictable? Not quite. In quantum mechanics, individual outcomes might not be predictable, but the odds of those outcomes are predictable. It’s kind of like a casino. They don’t know which particular players will win or lose, but they know very precisely what percentage will lose, so the casino will always make money. The baseball example was one of classical, everyday determinism. To include quantum mechanics we need a more general, probabilistic determinism known as quantum determinism, but the result is still the same. Information is conserved.

So what about black holes?

At first glance it would seem that black holes destroy information. If you toss an object into a black hole, the object (and all its physical information) is lost forever. It is as if the information of the object was erased, which would violate the basic principle that information cannot be destroyed. Now you might argue that being trapped is not the same thing as being destroyed, but for information it is. If you cannot recover the information, then it has been destroyed. So it would seem that black holes “eat” information, even though the laws of physics say that shouldn’t be possible. This is known as the black hole information paradox.

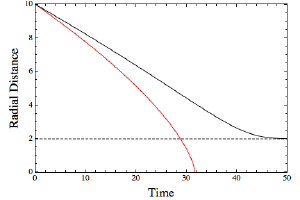
Brian Koberlein

But it turns out things are actually more subtle. In general relativity, once a black hole forms it exists forever. If more matter is thrown into it, it can grow larger, but it never goes away. This is important, because if black holes live forever they don’t actually destroy information. Since time is relative things get a bit strange. For example, if you were to toss your crime journal into a black hole, how long would it take to reach the event horizon? From the journal’s perspective, it will cross the event horizon and enter the black hole in a finite amount of time, but from the outside observer’s view the event horizon is never reached. Instead the journal appears to get ever closer at an ever slower pace. Any outside observer will see the time of the falling journal get slower and slower as the black hole warps spacetime more and more. From the outside it appears that the journal never quite enters the black hole, and so its information is never lost.

But suppose we took an object and compressed it into a black hole. According to general relativity, a black hole has three measurable properties: mass, rotation (angular momentum), and charge. That’s it. If you know those three things, you know all there is to know about the black hole. So a black hole is much simpler than other massive objects such as planets, stars and the like. It would therefore seem to have less information. If you think about an object like the Sun, it has a certain chemical composition, and it’s giving off light with different wavelengths having varying intensities. There are sunspots, solar flares, convection flows that create granules, and the list goes on. The Sun is a deeply complex object that we have yet to fully understand. The Sun contains a tremendous amount of information. And yet, if our Sun were compressed into a black hole, all that information would be reduced to mass, rotation and charge. All that information is lost forever.

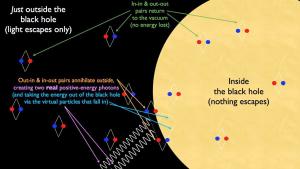
Ethan Siegel

But perhaps information can be saved by quantum theory. In the 1970s Stephen Hawking showed that one of the consequences of quantum theory is that black holes cannot hold matter forever. Instead, black holes can leak mass in the form of light and particles through a process known as Hawking radiation. While Stephen Hawking’s clever bit of mathematics describing this effect is pretty straightforward, interpreting the mechanism is less clear. One way of looking at it is that the Heisenberg uncertainty principle (which gives quantum theory its fuzzy behavior) means that virtual quantum particles can briefly appear in the vacuum of space, then then quickly disappear. In the normal, everyday world, these particles average out to zero, so we never notice them. But near the event horizon of a black hole, some of these virtual particles could cross the event horizon before disappearing, which decreases the mass (energy) of the black hole and allows other virtual particles to become “real” and radiate energy away. Another view is that the inherent fuzziness of quantum particles means you can never be absolutely certain that it is inside the event horizon. Although a particle cannot escape the black hole by crossing the event horizon, it could find itself outside the black hole through a kind of quantum tunneling.

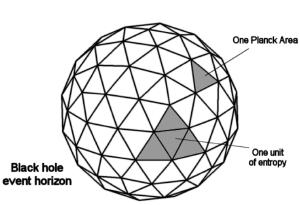Jacob D. Bekenstein

Since a “quantum” black hole emits heat and light, it therefore has a temperature. This means black holes are subject to the laws of thermodynamics. Integrating general relativity, quantum mechanics and thermodynamics into a comprehensive description of black holes is quite complicated, but the basic properties can be expressed as a fairly simple set of rules known as black hole thermodynamics. Essentially these are the laws of thermodynamics re-expressed in terms of properties of black holes. As with regular thermodynamics, the entropy of a black hole system cannot decrease. One consequence of this is that when two black holes merge, the surface area of the merged event horizon must be greater than the surface areas of the original black holes. But remember that thermodynamics and entropy are a way to describe the information of a system. Because black holes have entropy, they also contain information beyond the simple mass, rotation, charge. Perhaps the information isn’t destroyed after all!

Unfortunately there’s a snag. Just like any quantum process, Hawking radiation is probabilistically determined. But it’s determined by the basic properties of the black hole. According to Hawking’s original theory, when a black hole evaporates, it evaporates into a random mix of light and matter. Not just “kind of” random, like tossing a dice, but truly random. This eliminates any possibility of recovering information from a black hole. So it would seem Hawking radiation also destroys information.

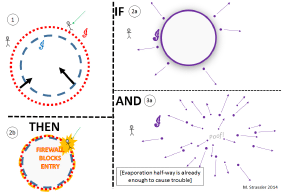Matt Strassler

But several people have looked at modifications to Hawking’s model that would allow information to escape. For example, because Hawking’s quantum particles appear in pairs, they are “entangled” (connected in a quantum way). Perhaps you can used this quantum connection to give the information a way to escape. It turns out that to allow Hawking radiation to carry information out of the black hole, the entangled connection between particle pairs must be broken at the event horizon, so that the escaping particle can instead be entangled with the information-carrying matter within the black hole. This breaking of the original entanglement would make the escaping particles appear as an intense “firewall” at the surface of the event horizon. This would mean that anything falling toward the black hole wouldn’t make it into the black hole. Instead it would be vaporized by Hawking radiation when it reached the event horizon. This is known as the firewall paradox.

It would seem then that either the physical information of an object is lost when it falls into a black hole (information paradox) or objects are vaporized before entering a black hole (firewall paradox). Basically these ideas strike at the heart of the contradiction between general relativity and quantum theory.

Can Hawking save us?

This brings us to Stephen Hawking, and all the hullabaloo about his announcement that he’s solved the information paradox. Has he? The truth is we don’t know, but probably not. Hawking knows his stuff, but so do lots of other folks who have been working on this problem for years with less media attention. So far no one has been able to crack this nut. Hawking also hasn’t released a formal paper yet. So not only is his idea not peer reviewed, it’s not even public. Until we see the details there will be more speculation than facts.

But we do know a few things about the idea, and one interesting aspect is the fact that it’s not a quantum model. It actually draws upon the ideas of thermodynamics. Time for a little history.

In the late 1800s Ludwig Boltzmann proposed that the properties of a gas, such as its temperature and pressure, were due to the the motion and interactions of atoms and molecules. This had several advantages. For example, the hotter a gas, the faster the atoms and molecules would bounce around, therefore temperature was a measure of the kinetic (moving) energy of the atoms. The pressure of a gas is due to the atoms and molecules bouncing off the walls of the container. If the gas is heated, the atoms move faster and bounce off the container walls harder and more frequently. This explains why the pressure of an enclosed gas increases when you heat it.

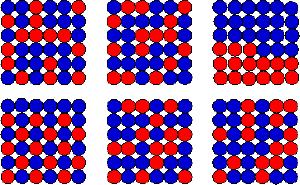Christine Nattrass

Boltzmann’s kinetic theory not only explained how heat, work and energy are connected, it also gave a clear definition of entropy. The pressure, temperature and volume of a gas is known as the state of the gas. Since these are determined by the positions and speeds of all the atoms or molecules in the gas, Boltzmann called these the microstate of the gas (the state of all the microscopic particles). For a given state of the gas, there are lots of ways the atoms could be moving and bouncing around. As long as the average motion of all the atoms is about the same, then the pressure, temperature and volume of the gas will be the same. This means there are lots of equivalent microstates for a given state of the gas.

But how do equivalent microstates relate to heat flowing from hot to cold? Imagine an ice cube in a cup of warm water. The water molecules in the ice cube are frozen in a crystal structure. This structure is pretty rigid, so there aren’t a lot of ways for the water molecules to move. This means the number of equivalent microstates is rather small. As the ice melts the crystal structure breaks down, and the water molecules are much more free to move. This means there are many more equivalent microstates for water than for ice. So heat flows into the ice, which increases the number of equivalent microstates, so the entropy of the system increases. The second law of thermodynamics applies both ways.

The idea of equivalent microstates can be applied to general relativity through an idea known as degenerate vacuua. The region outside a black hole (the vacuum) is the same for a black hole with a particular mass, rotation and charge. But lots of things could have gone into making the black hole, from stars to old issues of National Geographic. A black hole made of hydrogen, or neutrons, or iron all look the same from the outside, so we could say that each type of black hole is a microstate, and thus all the different ways we could make a black hole are therefore equivalent microstates. Or in general relativity terms, their exteriors are degenerate vacua.

These different vacua are related by a type of symmetry relation known as BCS symmetry, or supertranslations. What Hawking seems to be saying is that these supertranslations can be used to connect the information inside a black hole with the outside world. Basically, these degnenerate vacua bias the Hawking radiation so that it isn’t random. That way the information can escape without creating a firewall. If the idea works, then it might solve the information paradox. But even the little information released about the work has raised some serious doubts from other experts. It seems to be based upon an idealized black hole that doesn’t match real black holes, and it might not work even then. Either way, it’s up for Hawking and his colleagues to prove their case.

So we still don’t know whether black holes tell no tales.

If you’ve made it this far, congratulations. This is a deeply complex topic, and while I’ve done my best to explain what I understand about it, I won’t claim to be an authority. Fortunately lots of other scientists have written about it as well. For a few good summaries check out Sabine Hossenfelder, Ethan Siegel, and Matt Strassler.