Blog
The Numbers Game
26 April 2015
 Brian Koberlein
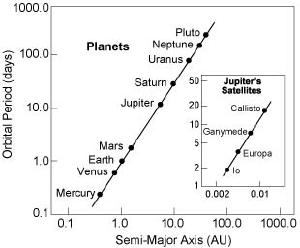
Brian KoberleinSuppose you measure the time a planet takes to orbit the Sun (its period), and compare it with a measure of its distance from the Sun (the semi-major axis). If you plot the logarithm of periods for all the planets (and even Pluto) vs the logarithm of their semi-major axes, you find they all lie along a line with a slope of 3/2. If you do the same for the moons of Jupiter, or Saturn, you get the same slope. The same is true for asteroids, comets, exoplanets and binary stars. They all follow the same 3/2 relation, and fall along the same line so long as they’re orbiting the same body.
 Kenneth R. Lang
Kenneth R. LangThis relation is true regardless of which scientific model we use to describe planetary motion. It is simply a description of the relationship between a planet’s period and distance. What makes the relation useful is its mathematical precision. Any theory of planetary motion should be able to derive this 3/2 relation as a consequence of the model. Not 4/3, not 8/5, but 3/2. It just so happens that Newton’s law of gravity makes just such a prediction. If we assume that masses are attracted to each other with a force inversely proportional to the square of their distance, then through a bit of calculus and geometry we can show the 3/2 relation must hold to an outstanding degree of precision.
There’s a reason why astronomical models are mathematical in nature. It’s only through mathematics that we can give precision to our description of the heavens. It’s one thing to say that planets close to the Sun orbit faster than more distant ones. It’s quite another to say, “how much faster?” To do that, we need to describe the relation mathematically.
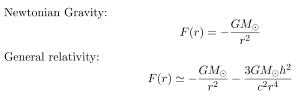 Brian Koberlein
Brian KoberleinWithout mathematical precision we have no way to distinguish between similar models. Take, for example, Newtonian gravity vs. general relativity. In Newton’s model, gravity is a simple force between masses. In general relativity gravity is a consequence of the warping of spacetime. While the description of gravity in these two models is radically different, both models derive the 3/2 relation for planetary motion. There’s actually very little to distinguish the models as far as planets are concerned.
 Wikipedia
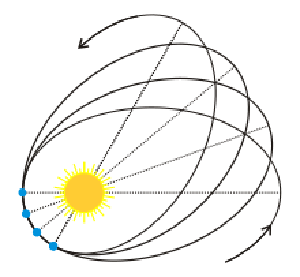
WikipediaThere are some small differences, such as their descriptions of the motion of Mercury. Both models predict that Mercury’s orbit will precess over time due to the gravitational interaction with other planets, but general relativity predicts Mercury will precess just a bit more. The difference in the two predictions is only about one-tenth of an arc second (which is 1/3600 of a degree) per orbit, but our measurements are precise enough to show that Einstein was right, and Newton was wrong.
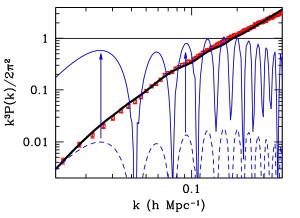
With mathematics, we can even test models we don’t entirely understand. While we don’t know the underlying cause for dark matter, we do understand the affect it must have on the way galaxies cluster together. We also know what affect alternative “modified gravity” models would have. Even with an incomplete understanding of either approach, we can look at what the mathematics of these models tell us.
 Scott Dodelson
Scott DodelsonWhat we find is that dark matter agrees with the clustering observations, while modified gravity does not. What’s more, the observational data best agrees with a specific form of dark matter known as cold dark matter. With mathematics, we don’t need to know everything about dark matter. We can simply derive the consequences of different assumptions and see what works. If we let the mathematics lead the way, we can often learn something about the universe.
Perhaps the most extreme case of letting the math lead us is in quantum theory. Despite its success as a scientific model for nearly a century, there is still a great deal of debate over the interpretation of quantum theory. Are there wavefunctions that collapse when observed? Does it imply the existence of parallel universes? The behavior of quantum systems are so deeply counterintuitive that we struggle to find a meaning behind the mechanism.
 Wikipedia
WikipediaHowever there is complete agreement on the mathematical formulation of quantum theory. The various interpretations of quantum theory rely upon the same mathematical results, which is why there’s no clear resolution to the argument. It’s also why a popular approach to teaching quantum theory is “shut up and calculate.”
While that might seem an unsatisfactory approach to scientific understanding, it’s produced the most precise scientific model ever devised. One property of the electron (and its heavier counterparts, the muon and tau) is its magnetic moment, which is often expressed in terms of a dimensionless g-factor. Experimentally this g-factor has a value of 2.0023318416, accurate to 0.26 parts per trillion. The predicted value from quantum electrodynamics (QED) is 2.0023318361. The difference is only 5 parts in a billion, but even that may be enough to hint at deeper physics yet to come.
 Particle Zoo
Particle ZooWhen we talk about astrophysics to the general public, we often rely on appealing images and rough analogies to convey the meaning behind the mathematics. It’s a good way to convey our understanding of the universe, but it also gives the impression that the analogies are what science is all about. This is why so many “alternative” science promoters focus on broad concepts. “Clearly dark matter is due to plasma tubes!” they’ll say. “Black holes are just concentrated unobtainium!” The idea is the key, and the mathematics is left as an exercise for the reader.
For real scientific models, however, the mathematics is central, and the ideas are a useful way to lead you toward the mathematical formalism. Its the unity of physical models and mathematical formalism that produces the most powerful and accurate scientific models. Precision is key, and without it, science is merely a numbers game.