Blog
The Strangest Theory
We Know Is True
12 January 2015
When you think of the strangest scientific theory ever, you probably think of quantum mechanics. With its particle-wave duality and collapsing wavefunctions, it can certainly be considered a strange theory. But I would argue that even more bizarre is the theory of relativity. In quantum theory objects behave strangely in space and time, but in relativity the very nature of space and time is questioned. Despite all of its consequences such as curved space, time dilation and interchange of mass and energy, we know relativity to be true. Not just “kind of” true, but provably true to a high degree of precision.
 Case Western Reserve Archive
Case Western Reserve ArchiveThe foundational experiment for both special and general relativity is the verification that the speed of light in a vacuum is the same for all frames of reference. This was first demonstrated by the famous Michelson-Morley experiment in 1887. The idea that the speed of light is constant is deeply counterintuitive. It would be as if you are riding a skateboard at 5 mph, and you toss a ball at 15 mph, and someone standing on the sidewalk sees the ball move not at 20 mph, but 15 mph just as you do. Michelson and Morley weren’t trying to prove light speed is constant, they were actually trying to determine how the speed of light changes as the Earth orbits the Sun. Instead of observing a changing speed of light, they found no variation to the limit of their experiment, which was about 1 part in 40,000. Because of this, the Michelson-Morley experiment is sometimes called the most successful failed experiment ever.
Since then, the result has been confirmed numerous times. With the advent of lasers, the experiment could be performed to extremely high accuracies. The results were so precise that in 1983 the speed of light became the standard by which the meter is defined. The most recent tests of the constancy of light speed find that it varies by no more than a few parts per quintillion.
Since the speed of light is constant for all frames of reference, there should be a difference between the way time is observed in different reference frames. We can see how this works if we imagine a clock made with light. Take two mirrors and place one above the other and facing each other, then bounce a pulse of light between them. We can measure time by counting the number of times the light bounces off a mirror. Each bounce is like the tick or tock of a mechanical clock. If you could watch the pulse of light, you would see it move up and down between the mirrors at the speed of light. Up and down at a constant rate. Now suppose you took your clock on a fast moving train. Standing in the aisle of the train, you would see the light pulse move up and down at the same rate as before. Up and down at the speed of light.
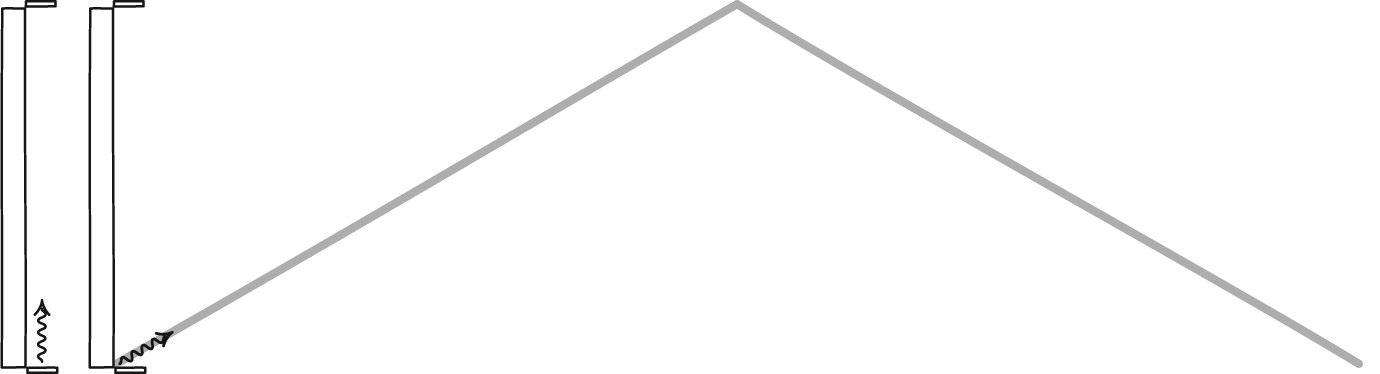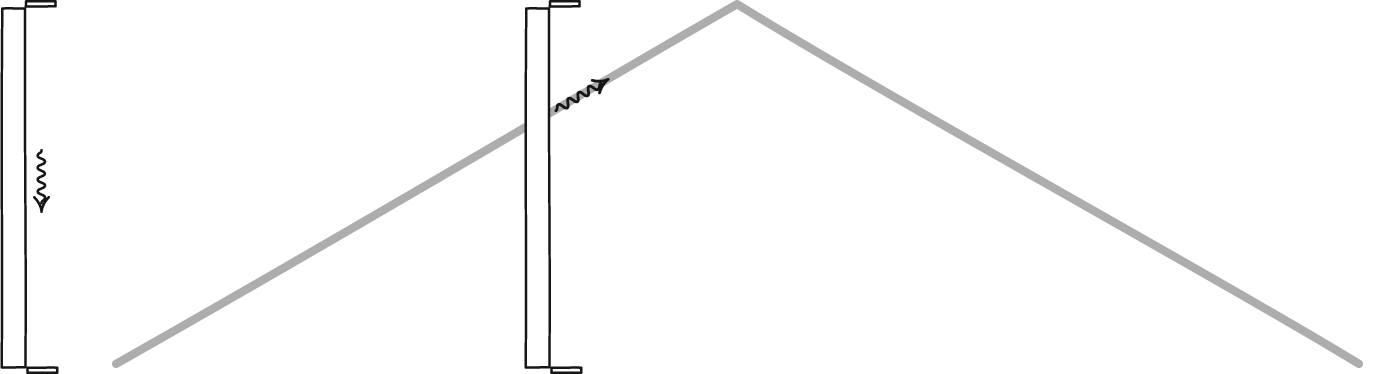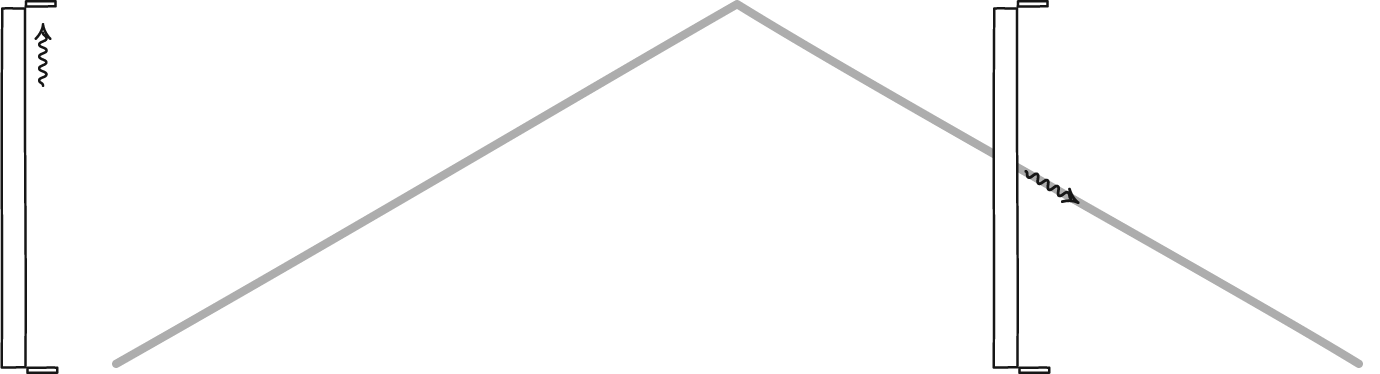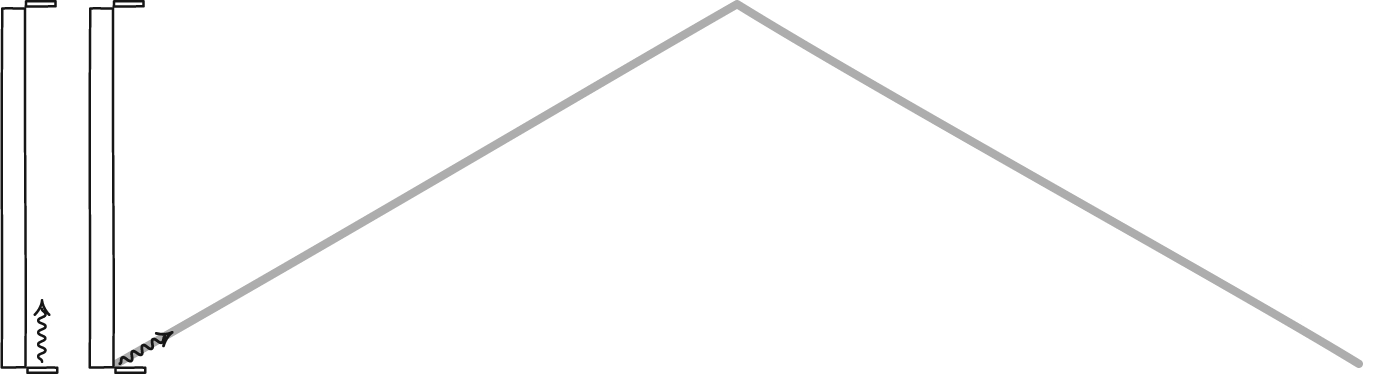 John D. Norton
John D. NortonBut an observer watching the train pass by would see something slightly different. They would also see the pulse move at the speed of light, but from their perspective the light can’t move straight up and down because it must also be moving along with you. They would see the pulse move diagonally up then diagonally down, which is a slightly longer distance between each bounce. That means it would take the light longer to travel from bounce to bounce. So from their viewpoint the ticks and tocks of your clock are slower than the ticks and tocks as you see them. Your clock appears to be running slow because of your motion relative to them.
This effect is known as time dilation, and it can be demonstrated by what is known as the Ives–Stilwell experiment. This experiment looks at the light emitted or absorbed by fast moving particles and compares them with the transverse Doppler effect. If an object speeds past you from left to right, when it is directly in front of you would you see any Doppler shift of its light? Since the relative motion along your line of sight at that moment is zero, you might think there would be no shift. But since the object is speeding past you, its time should be dilated. As a result there should be a Doppler shift. The Ives-Stilwell experiment is thus a direct test of time dilation. It was first performed in 1938, and has been improved upon over the years. Just this week, results on a new version of the experiment has confirmed time dilation to 2 parts in a billion.1
Other experiments have looked at time dilation by comparing the time of two clocks in motion relative to each other. These experiments assume light obeys special relativity, so they are model dependent rather than the direct Ives-Stilwell experiments. However when comparing the relative time dilation of two atomic clocks, we find that they agree with the predictions of relativity to within one part in 1016. Special relativity makes our observations of space and time relative, but it is astoundingly accurate.
Of course relativity can be broadened to include the effects of gravity. This general theory of relativity begins with the observation that any two objects will fall in a gravitational field in the same way. It was first noted by Galileo who (according to legend) dropped lead balls of different size from the tower of Pisa. Galileo actually tested the idea by rolling balls down an inclined plane, and could find no observable difference.
 Missouri Science & Tech
Missouri Science & TechIn 1908 Loránd Eötvös made the first precision test of the equivalence principle using a torsion balance, and found that it was true to within one part in a billion. Over the last century this result has been improved to the point that we now know the equivalence principle is true to within 1 part in 1014.
Using the equivalence principle, Einstein developed a gravitational theory even more strange than special relativity. In his theory the fabric of space and time can be bent and twisted by the presence and motion of masses. One of the first tests of the gravitational curvature of space was the deflection of starlight during a solar eclipse, first observed by Eddington in 1919. Eddington’s results supported Einstein’s model, but not very strongly. Given the radical approach of general relativity, Eddington’s results were initially disputed by some. But subsequent observations confirmed Einstein’s predictions.
 ESA/Hubble & NASA
ESA/Hubble & NASAThe most recent tests of light bending agree with general relativity to within 0.3%. That doesn’t seem very strong, but it’s very difficult to measure accurately. At Earth’s distance, the light of a star seen at a direction 90° away from the Sun is deflected by 4 milliarcseconds. That’s roughly equivalent to the width of a human hair seen from 3 kilometers away.
Our astronomical instruments have gotten so precise that even this small deflection must be taken into account. Satellites such as Hipparcos (and soon Gaia) make very precise observations of the positions of millions of stars. As the satellites orbit the Sun, measured stars are sometimes aligned more closely or more distant from the Sun. As a result, the gravitational curvature of the Sun can shift the observed position of the stars by a measurable amount. In fact, measurements of Gaia will be so precise that it could provide a more stringent confirmation of light bending.
Perhaps the weirdest prediction of relativity is that rotating masses twist space around them. This effect is known as frame dragging, and it is most dramatic around black holes. But even the Earth’s rotation twists space ever so slightly. In 2011 a spacecraft known as Gravity Probe B successfully observed this effect due to the Earth.
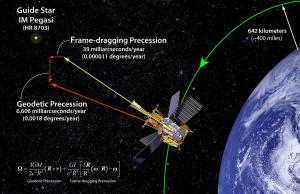 Gravity Probe B Team, Stanford, NASA
Gravity Probe B Team, Stanford, NASAThe frame dragging effect of Earth is so small that it’s astounding we can perceive it at all. To observe these effects, the team had to create quartz spheres so precise that their surface varied no more than 40 atoms from a mathematically perfect sphere. They were then covered with a thin layer of niobium so they could be suspended within an electric field. Their rotation created a small magnetic field, which was measured by superconducting quantum interference devices. Of course all of this is packed into a probe and shot into space for an 18 month mission. Over the duration of the experiment, the rotation of the spheres had to be measured with milliarcsecond precision. Despite the challenges, Gravity Probe B confirmed the Earth’s gravitational curvature of space to within 1% of predictions, and confirmed frame dragging to within 19%.
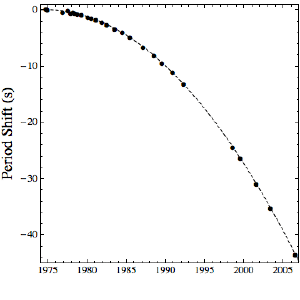 Brian Koberlein
Brian KoberleinDespite all these successes, there is one confirmation of relativity which still eludes us: direct observation of gravitational waves. According to general relativity, when large masses such as neutron stars or black holes orbit each other, they should create ripples in spacetime. These ripples should radiate outward as gravitational waves. Because these waves carry energy away from the system, the orbits of these massive objects should decay. We’ve seen this kind of orbital decay in binary pulsars, so we’re pretty certain these gravitational waves exist. But to truly be certain we’d like to detect them directly.
In principle we should be able to observe their effect as an oscillation in the separation distance of two mirrors. But even if the mirrors were separated by 4 kilometers, the variation in their distance would only be about 10-18 meters, or about a thousand times smaller than the width of a proton. We haven’t confirmed gravitational waves yet, but with projects such as LIGO, and the proposed space-based LISA, we will likely succeed.
Of course, these experiments are only possible using lasers, and the knowledge of the invariant speed of light. Perhaps it is fitting that we use the first triumph of relativity to strive for its last great confirmation.
Botermann, Benjamin, et al. “Test of time dilation using stored Li+ ions as clocks at relativistic speed.” Physical Review Letters 113.12 (2014): 120405. ↩︎